斜率相等的协方差分析的示例
使用“拟合模型”平台的“标准最小二乘法”特质拟合协方差分析模型。协方差分析模型是包含关注的主因子和协变量项的模型。协变量是所关注主因子之外的因子,但可能影响主因子对响应的效应。在本例中,药物是关注的主因子,x 是协变量。
注意:该分析假设协变量以相似的方式影响主因子的每个水平。即:协方差模型的斜率相等。模型中不包含交互作用项。关于斜率不等的模型,请参见斜率不等的协方差分析的示例。
1. 选择帮助 > 样本数据文件夹,然后打开 Drug.jmp。
2. 选择分析 > 拟合模型。
3. 选择 y 并点击 Y。
4. 选择药物和 x,然后点击添加。
5. 点击运行。
下面显示报表各个部分及说明。
回归图和“预测值-实际值”图
使用回归图和“预测值-实际值”图来评估模型并了解协变量对响应的影响。
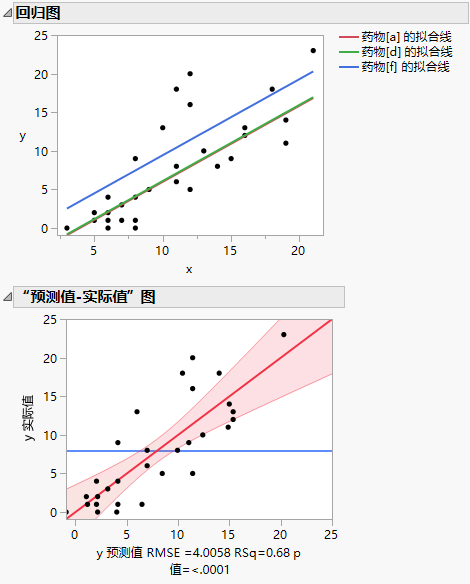
图 4.20 斜率相等的协方差分析图
“回归图”显示您拟合了一个斜率相等的模型。对于每种药物,响应都以相同的速率随协变量 x 增加。在协变量 x 的各个水平中,对药物 f 的响应最高。
失拟
药物数据表包含重复的观测。例如,第 1 行和第 9 行都包含药物 = a 且 x = 11。在拟合模型时,重复的观测可用于构造变异的纯误差估计值。可以为未指定函数形式的协变量或名义型效应的交互作用构造另一种误差估计值。这些估计值构成失拟检验的基础。若失拟误差显著,这指示模型未能解释数据中的某个效应。请参见失拟。
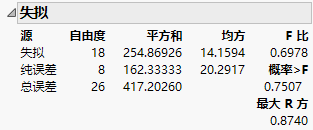
图 4.21 斜率相等的协方差分析“失拟”检验
“失拟”报表显示:失拟误差不显著,“概率>F”值 0.7507 证实了这一点。
最小二乘均值
使用最小二乘均值比较药物的每个水平的平均响应(将协变量考虑在内)。
最小二乘均值不同于普通均值,这是因为前者已针对协变量在响应上的效应进行了调整。最小二乘均值是当协变量 x 具有均值 10.7333 时,为药物三个水平中的每个水平预测的值。
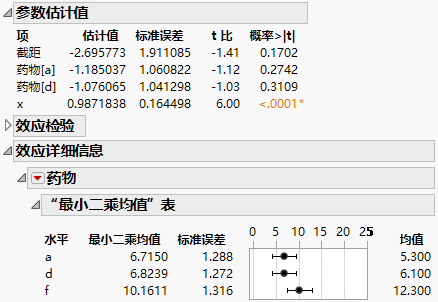
使用“参数估计值”报表中给出的参数估计值计算最小二乘均值:
预测表达式:
-2.696 - 1.185*药物[a] - 1.0761*药物[d] + 0.98718*x
对于 a:
-2.696 - 1.185*(1) -1.0761*(0) + 0.98718*(10.7333) = 6.71
对于 d:
-2.696 - 1.185*(0) -1.0761*(1) + 0.98718*(10.7333) = 6.82
对于 f:
-2.696 - 1.185*(-1) -1.0761*(-1) + 0.98718*(10.7333) = 10.16
图 4.22 药物检验数据的参数估计值和最小二乘均值