启动“广义线性混合模型”特质
启动“广义线性混合模型”特质
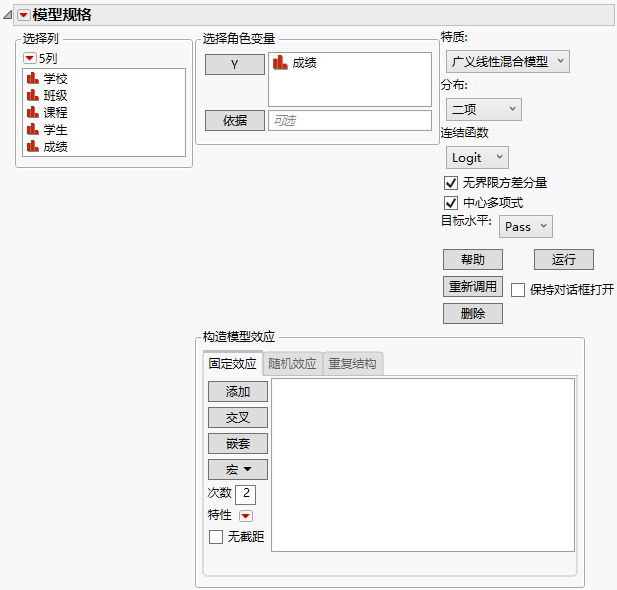
通过以下方式启动“广义线性混合模型”特质:选择分析 > 拟合模型,输入一个或多个 Y 列,然后从特质菜单选择广义线性混合模型。
 “拟合模型”启动窗口
“拟合模型”启动窗口
您可以指定带有固定效应、随机效应或固定与随机效应组合的模型。还可以指定响应变量的分布。启动窗口中的选项根据您所指定的模型的性质而有所不同。有关“选择列”红色小三角菜单中选项的详细信息,请参见《使用 JMP》中的“列过滤器”菜单。
使用“广义线性混合模型”特质拟合模型时,您可以允许无界限方差分量。这意味着具有负估计值的方差分量不被报告为零。默认选定该选项。若您关注的是固定效应,则它应保持选定状态,因为将方差估计值的边界定为零将导致固定效应检验发生偏倚。有关“无界限方差分量”选项的详细信息,请参见负方差。
图 9.6 选择了“广义线性混合模型”的“拟合模型”启动窗口
有关对所有特质通用的“拟合模型”窗口各方面的详细信息,请参见模型规格。有关“选择列”红色小三角菜单中选项的详细信息,请参见《使用 JMP》中的“列过滤器”菜单。这里提供“广义线性混合模型”特质特有的信息。
 指定分布
指定分布
在“拟合模型”启动窗口中,将“广义线性混合模型”选作“特质”时即会显示“分布”选项。在此您可以指定 Y 的分布。下面说明了可用的分布。
正态
指定 Y 服从均值为 m 且标准差为 s 的正态分布。正态分布是对称的,若样本足够大,很多其他分布可以使用中心极限定理将其近似为正态分布。m 的连结函数是恒等,即,Y 的均值表示为线性模型。
指数
指定 Y 服从均值参数为 m 的指数分布。指数分布是向右偏斜的,通常用于对寿命或两个相继事件之间的时间建模。m 的连结函数为对数。
Gamma
指定 Y 服从均值参数为 m 且离散参数为 s 的 gamma 分布。gamma 分布很灵活,它包含一系列其他广泛使用的分布。例如,指数分布是 gamma 分布的特例,其中 s = m。卡方分布也可以从 gamma 分布导出。m 的连结函数为对数。
对数正态
指定 Y 服从位置参数为 m 且尺度参数为 s 的对数正态分布。对数正态分布是向右偏斜的,通常用于对寿命或事件发生前的时间建模。m 的连结函数是恒等。
Beta
指定 Y 服从均值参数为 m 且离散参数为 s 的 beta 分布。beta 的响应介于 0 到 1 之间(不包括 0 和 1),通常用于比例或比率建模。m 的连结函数为 Logit。
二项
指定 Y 服从参数为 p 和 n 的二项分布。响应 Y 指示所有试验中具有固定概率 p 的 n 个独立试验中的总成功次数。该分布允许使用样本大小列。若未列出任何列,则假定样本大小为 1。默认情况下,p 的连结函数为 Logit。您可以使用“拟合模型”启动窗口中的“连结函数”选项将 p 的连结函数更改为 Probit。若选择建模类型为“名义型”的二值响应变量,则只有“二项”是可用的响应分布。
当您选择“二项”作为“分布”时,必须使用以下方式之一指定响应变量。
‒ 未汇总:若您的数据未汇总为事件频数,指定一个二值列作为响应。若该列的建模类型为名义型,那么您可将其中一个水平指定为“目标水平”。默认“目标水平”值是基于水平顺序的两个水平中的较高者。
‒ 已汇总且将样本大小列输入为第二个 Y:若您的数据已汇总为事件(成功)和试验的频数,则按如下顺序将两个连续列指定为 Y:成功次数的计数和试验次数的计数。
Poisson
指定 Y 服从均值为 l 的 Poisson 分布。Poisson 分布通常对给定时间间隔中的事件数建模,经常表示为计数数据。l 的连结函数为对数。即使 Y 采用非整数值,Poisson 回归也是允许的。
负二项
指定 Y 服从均值为 m 且离散参数为 s 的负二项分布。负二项分布通常对指定失败次数之前的成功次数建模。负二项分布也等价于某些条件下的 Gamma Poisson 分布。有关负二项和 Gamma Poisson 之间关系的详细信息,请参见《基本分析》中的分布。
运行 JMP Samples/Scripts 文件夹中的 demoGammaPoisson.jsl,将具有均值 l 和离散参数 s 的 Gamma Poisson 分布与具有均值 l 的 Poisson 分布进行比较。
m 的连结函数为对数。即使 Y 采用非整数值,负二项回归也是允许的。
下表提供了被分配各种分布的 Y 变量的数据类型、建模类型和其他要求。
分布 | 数据类型 | 建模类型 | 其他 |
|---|---|---|---|
正态 | 数值 | 连续 |
|
指数 | 数值 | 连续 | 非负 |
Gamma | 数值 | 连续 | 正值 |
对数正态 | 数值 | 连续 | 正值 |
Beta | 数值 | 连续 | 介于 0 到 1 之间 |
二项,未汇总 | 任意 | 任意 | 二值 |
二项,已汇总且将计数列输入为第二个 Y | 数值 | 连续 | 非负 |
Poisson | 数值 | 任意 | 非负 |
负二项 | 数值 | 任意 | 非负 |
下表提供分布参数化和连结函数的汇总。
分布 | 参数 | 均值模型连结函数 |
|---|---|---|
正态 | m, s | 恒等(m) |
指数 | m | Log(m) |
Gamma | m, s | Log(m) |
对数正态 | m, s | 恒等(m) |
Beta | m | Logit(m) |
二项 | n, p | Logit(p) Probit(p) |
Poisson | L | Log(m) |
负二项 | m, s | Log(m) |
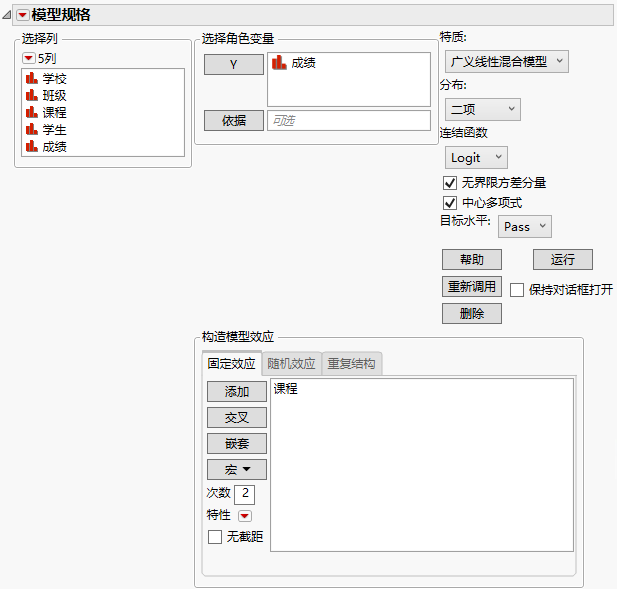
 “固定效应”选项卡
“固定效应”选项卡
在“固定效应”选项卡上添加所有固定效应。根据需要使用“添加”、“交叉”、“嵌套”、“宏”和“特性”选项。有关这些选项的详细信息,请参见模型规格。请注意,模型中可能没有固定效应。
注意:若连续列涉及随机效应,则该列不会位于中心,即使选择了“模型规格”红色小三角菜单中的“中心多项式”选项也是如此。
图 9.7 显示“固定效应”的完成的“拟合模型”启动窗口
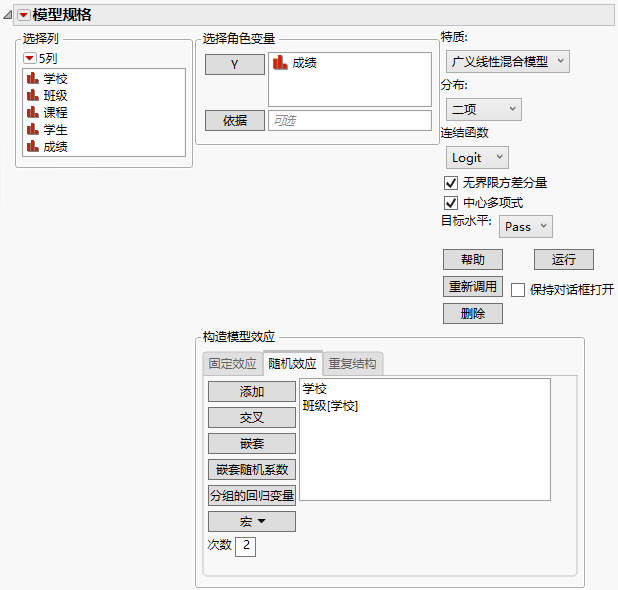
 “随机效应”选项卡
“随机效应”选项卡
使用“随机效应”选项卡指定传统方差分量模型和随机系数模型。
注意:若连续列涉及随机效应,则该列不会位于中心,即使选择了“模型规格”红色小三角菜单中的“中心多项式”选项也是如此。
方差分量
对于传统方差分量模型,使用“添加”、“交叉”或“嵌套”选项指定如随机区组、整区误差项和子区误差项之类的项。有关这些选项的详细信息,请参见模型规格。
图 9.8 显示“随机效应”的已完成“拟合模型”启动窗口
随机系数
要构造随机系数模型,使用“嵌套随机系数”按钮来创建随机系数组。
1. 从“选择列”列表中选择作为预测变量的连续列。
2. 选择随机效应选项卡,然后点击添加。
3. 在“随机效应”选项卡中选择这些效应。还选择包含随机效应的列,该效应的水平定义各回归模型。
4. 点击嵌套随机系数按钮。
最后一步创建在随机效应的各个水平内有相关性的随机截距和随机斜率效应。由于对象间的变异性,对象嵌套在其他效应内。若您相信截距可能对所有组是固定的,可以选择截距[<组>]&随机系数(1),然后点击删除。
您可以按该方式定义多个随机系数组,如在层次线性模型中那样。当斜率和截距系数具有随机批次效应和处理*随机批次效应时,这可能是必要的。在以下层次线性模型中这也可能是必要的:学习成绩具有随机学生效应和随机学校效应,并且学生嵌套在学校内。
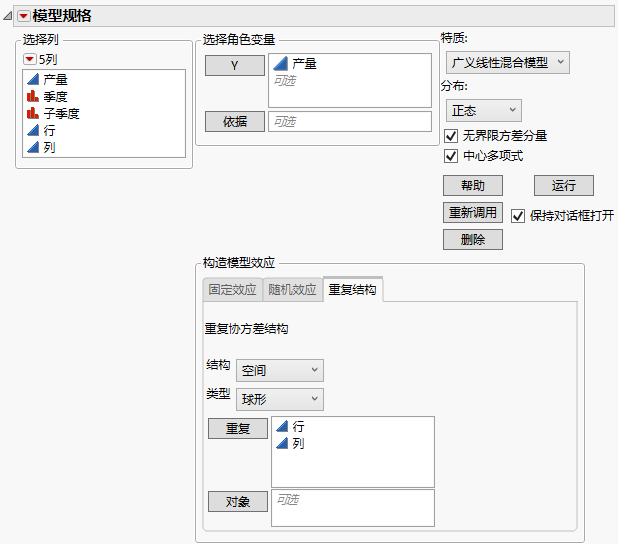
 “重复结构”选项卡
“重复结构”选项卡
使用“重复结构”选项卡来选择模型中重复效应的协方差结构。
表 9.3 显示“重复结构”选项卡的完成的“拟合模型”启动窗口
结构
重复结构默认设置为“无”。“无”结构指定观测值之间没有协方差,即误差是独立的。所有其他协方差结构都对观测之间的协方差建模。
Table 9.4 列出了可用的协方差结构、使用每个结构的要求以及给定结构的协方差参数个数。观测次数用 J 表示。
结构 | 重复列类型 | 所需的重复列数目 | 对象 | 参数个数 |
|---|---|---|---|---|
无 | 不适用 | 0 | 不适用 | 0 |
非结构化 | 分类 | 1 | 必需 | J(J+1)/2 |
AR(1) | 连续 | 1 | 可选 | 2 |
复合对称性 | 分类 | 1 | 必需 | 2 |
Toeplitz | 分类 | 1 | 必需 | J |
事前相关 | 分类 |
| 必需 | 2J-1 |
空间 | 连续 | 2+ | 可选 |
|
若您输入具有“无”结构的重复列或对象列,将忽略这些列。显示以下警报:“当选择残差协方差结构时忽略重复列和对象列。”
类型
当您选择“空间”协方差结构时,将显示一个“类型”列表,您可以在其中选择空间结构的类型。提供四种类型:“乘方”、“指数”、“高斯”和“球形”。
重复
输入定义重复测量结构的列。“重复”列的建模类型取决于协方差结构。有关每个重复测量协方差结构的要求的详细信息,请参见Table 9.4。
对象
输入定义对象的一个或多个列。“对象”列必须是分类的。
 数据格式
数据格式
“拟合模型”平台的“广义线性混合模型”特质要求所有响应测量值都包含在一个响应列中。重复测量数据有时记录在多个列中,其中,每行都是一个对象,重复的测量值记录在单独的响应列中。必须在运行“广义线性混合模型”特质之前堆叠该格式的数据。Cholesterol.jmp 和 Cholesterol Stacked.jmp 样本数据表分别演示了宽格式和堆叠格式。请注意,宽表中的每行都对应于堆叠表中患者的一个水平。