主成分

主成分分析的目的是要从一组测量变量中得到少数几个相互独立的线性组合（主成分），使用它们来捕获原始变量中尽可能多的变异性。主成分分析是一种降维方法，也是一种探索性数据分析工具。主成分分析也可用于构造预测模型，如主成分分析回归（亦称 PCA 回归或 PCR）所述。

“主成分”平台提供两类用于获取主成分的方法。传统方法使用协方差矩阵、相关性矩阵或未统一尺度且未中心化的矩阵获取主成分。高级方法使用多种奇异值分解技巧来获取主成分。

高级方法适用于具有大量变量的数据，这些方法支持您以高效的计算时间计算主成分。多数高级方法都要求您指定要估计的成分数。成分数通常远小于数据的维。随后可将这些主成分用在 PCA 回归中。

“主成分”平台还支持因子分析。JMP 提供若干类型的正交和斜交因子分析样式的旋转，用来帮助解释提取的成分。有关因子分析的信息，请参见因子分析。

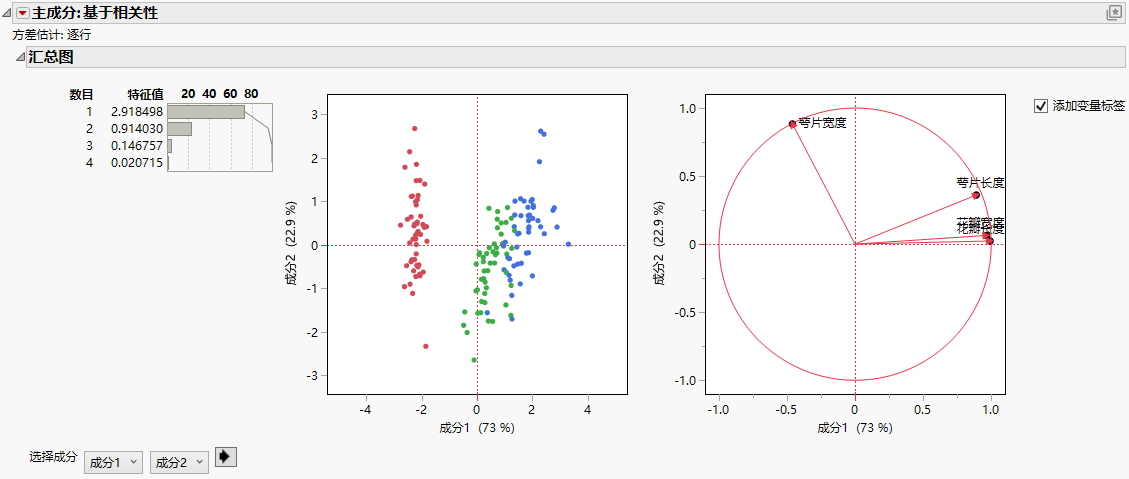
图 4.1 主成分示例

此处显示图片

目录