直接模型拟合的统计详细信息
“函数数据分析器”平台中的直接模型拟合依赖于矩阵分解。数据被转换为堆叠矩阵。矩阵的每一行对应于 ID 变量的一个水平的完整输出函数，矩阵的每一列对应于输入变量的一个水平。直接模型通过对函数的堆叠矩阵执行某种类型的矩阵分解例程来获取函数主成分分析 (FPCA) 结果。在多种直接方法中使用的其中一种矩阵分解是奇异值分解 (SVD)。
n x p 矩阵 X 的 SVD 可表示为：
X ≈ UDV′
矩阵 U、D 和 V 具有以下属性：
• U 是得分的 n x r 正交矩阵且 U′U = Ir。
• V 是载荷的 p x r 正交矩阵且 V′V = Ir。
• D 是正奇异值的 r x r 对角线矩阵，表示为 sk。
• r << min(n, p)
V 的列对应于形状函数，奇异值对应于特征值。数据中的每个函数使用形状函数（V 的列）的线性组合来近似。
惩罚 SVD
惩罚 SVD 方法一次对堆叠函数的矩阵分解一维。在奇异值分解 (SVD) 方法中，这意味着查找 X 的最佳秩一近似。近似 X 的秩一近似等价于最小化平方 Frobenius 范数，其表示为：
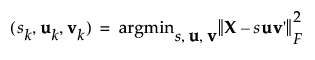
加入惩罚参数之后，最小化函数表示为：
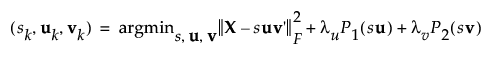
其中 P1(su) 和 P2(sv) 是引起稀疏性的惩罚参数。
对于每个维 k，执行以下例程：
1. 执行标准 SVD 以获得起始值。
2. 修复 u 并执行带 lasso 惩罚的惩罚回归来求解 v，使用 AICc 进行验证。
3. 修复 v 并执行带 lasso 惩罚的惩罚回归来求解 u，使用 AICc 进行验证。
4. 重复step 2和step 3，直到 u 和 v 收敛。
有关详细信息，请参见 Lee et al (2010)。
非负 SVD
“非负 SVD”方法对函数的堆叠矩阵执行奇异值分解 (SVD)，包含以下其他约束：
X ≈ UDV′ 其中 Uij ≥ 0 且 Vij ≥ 0
该方法使用约束的最小二乘法来求解 U 和 V。
多元曲线分辨率
“多元曲线分辨率”(MCR) 方法也使用矩阵分解，但将函数的堆叠矩阵分解为两个而不是三个矩阵。n x p 矩阵 X 的矩阵分解可表示为：
X ≈ CS′
矩阵 C 和 S 具有以下属性：
Cij ≥ 0
Sij ≥ 0
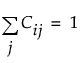，因此 C 的每一行的总和为 1
S 的列是非负形状函数，C 的行是混合比例。这将创建 X 的近似，其中对于每个单独的函数，得分总和为 1，函数是形状函数的混合函数。