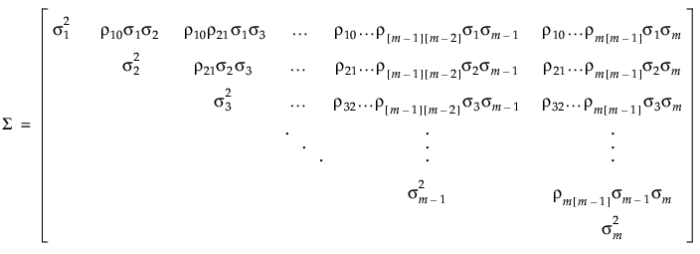在此,在时间 j 获取的观测值之间的方差为:
在此,在时间 j 获取的观测值之间的方差为:
|
•
|
|
•
|
在此,tj 是观测值 j 的时间。在该结构中,在任意给定时间取的观测具有相同方差 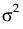 。参数 ρ(其中 -1 < ρ < 1)是相隔一个时间单元的两个观测之间的相关性。随着观测值之间的时间差异增大,其协方差会下降,因为 ρ 上升到更高次幂。在很多应用中,AR(1) 提供对象内相关性的适当模型,提供更高功效而不会降低对第一类错误的控制。
。参数 ρ(其中 -1 < ρ < 1)是相隔一个时间单元的两个观测之间的相关性。随着观测值之间的时间差异增大,其协方差会下降,因为 ρ 上升到更高次幂。在很多应用中,AR(1) 提供对象内相关性的适当模型,提供更高功效而不会降低对第一类错误的控制。
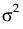 。参数 ρ(其中 -1 < ρ < 1)是相隔一个时间单元的两个观测之间的相关性。随着观测值之间的时间差异增大,其协方差会下降,因为 ρ 上升到更高次幂。在很多应用中,AR(1) 提供对象内相关性的适当模型,提供更高功效而不会降低对第一类错误的控制。
。参数 ρ(其中 -1 < ρ < 1)是相隔一个时间单元的两个观测之间的相关性。随着观测值之间的时间差异增大,其协方差会下降,因为 ρ 上升到更高次幂。在很多应用中,AR(1) 提供对象内相关性的适当模型,提供更高功效而不会降低对第一类错误的控制。在 Toeplitz 结构中,用固定的时间单位数分隔的观测具有相同的相关性。对比 AR(1) 相关性结构,固定时间差值处的 Toeplitz 相关性是任意的。用 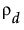 表示相隔 d 个单元的观测的相关性。相关性矩阵如下所示:
表示相隔 d 个单元的观测的相关性。相关性矩阵如下所示:
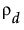 表示相隔 d 个单元的观测的相关性。相关性矩阵如下所示:
表示相隔 d 个单元的观测的相关性。相关性矩阵如下所示:|
•
|
 重复的协方差结构
重复的协方差结构 不等方差协方差结构
不等方差协方差结构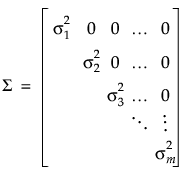
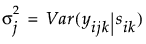
 非结构化协方差结构
非结构化协方差结构

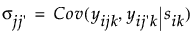
 复合对称性协方差结构
复合对称性协方差结构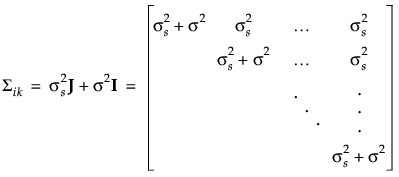
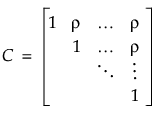
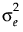 。则协方差结构为
。则协方差结构为 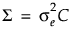 ,其中
,其中

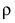 是组内相关系数,
是组内相关系数,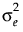 为残差方差。另一选项是在 JMP 中使用“复合对称性不等方差”结构,该结构允许方差随时间点变化。这导致协方差矩阵如下所示:
为残差方差。另一选项是在 JMP 中使用“复合对称性不等方差”结构,该结构允许方差随时间点变化。这导致协方差矩阵如下所示:
 AR(1) 协方差结构
AR(1) 协方差结构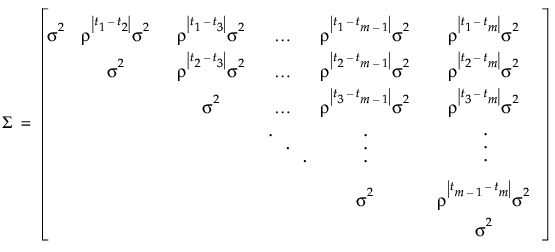
 Toeplitz 协方差结构
Toeplitz 协方差结构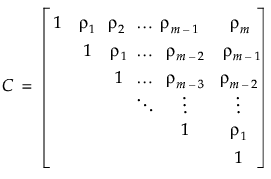
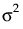 。协方差结构为
。协方差结构为 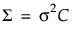 。
。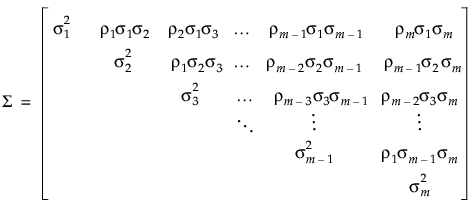
 事前相关协方差结构
事前相关协方差结构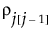 。
。
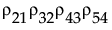 。
。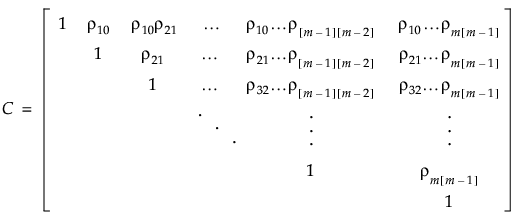
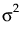 ,协方差矩阵为
,协方差矩阵为 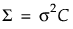 。
。 , 则协方差矩阵如下所示:
, 则协方差矩阵如下所示: