This example, adapted from Meyer, et al. (1996), demonstrates how to use the augment designer in JMP to resolve ambiguities left by a screening design. In this study, a chemical engineer investigates the effects of five factors on the percent reaction of a chemical process.
To begin, open Reactor 8 Runs.jmp found in the Design Experiment sample data folder installed with JMP. Then select Augment Design from the DOE menu. When the initial launch dialog appears:
|
1.
|
|
2.
|
|
3.
|
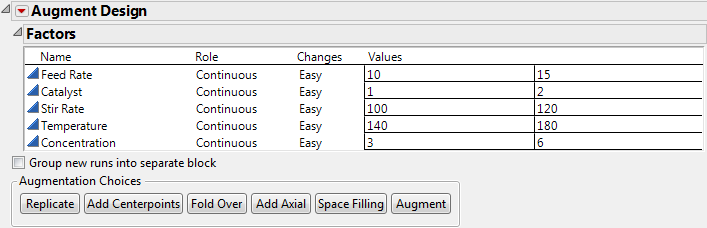
Click OK on the launch dialog to see the Augment Design dialog in Augment Design Dialog for the Reactor Example.
|
Note: You can check Group new runs into separate block to add a blocking factor to any design. However, the purpose of this example is to estimate all two-factor interactions in 16 runs, which cannot be done when there is the additional blocking factor in the model.
|
4.
|
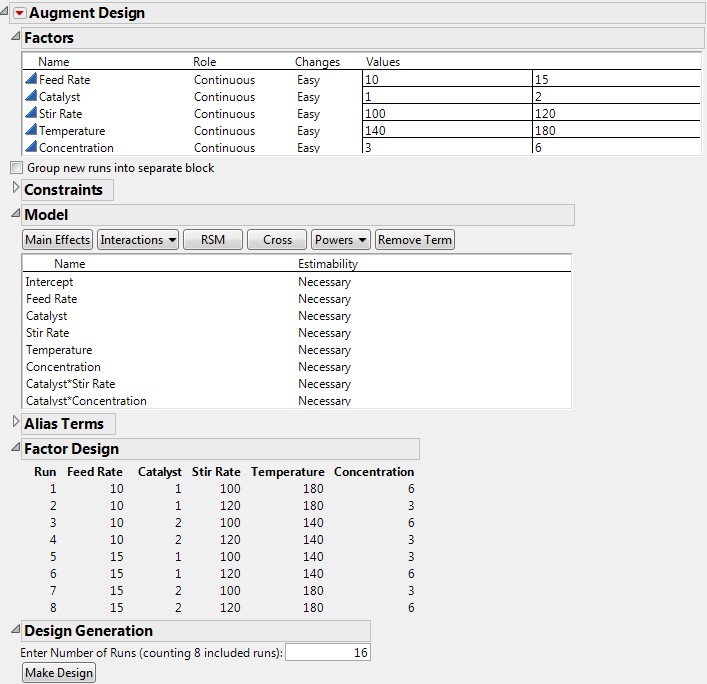
This model shown in Initial Augmented Model is the result of the model stored with the data table when it was created by the Custom designer. However, the augmented design is to have 16 runs in order to estimate all two-factor interactions.
|
5.
|
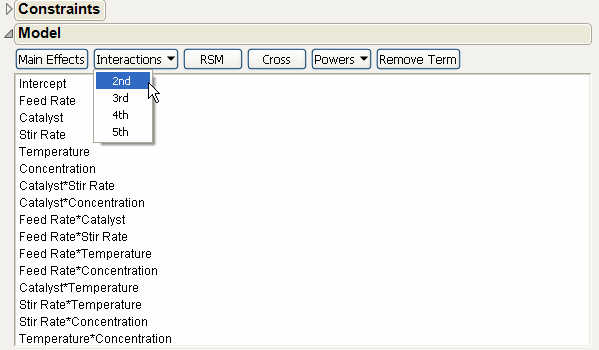
Choose 2nd from the Interactions menu as shown in Augmented Model with All Two-Factor Interactions. This adds all the two-factor interactions to the model. The Minimum number of runs given for the specified model is 16, as shown in the Design Generation text edit box.
|
|
6.
|
Click Make Design.
|
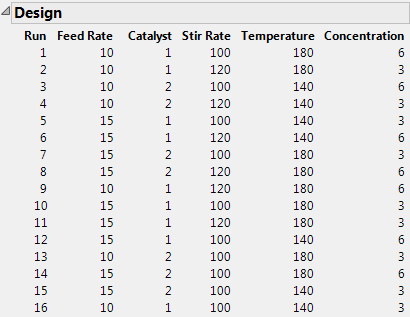
JMP now computes D-optimally augmented factor settings, similar to the design shown in D-Optimally Augmented Factor Settings.
Note: The resulting design is a function of an initial random number seed. To reproduce the exact factor settings table in D-Optimally Augmented Factor Settings, (or the most recent design that you generated), choose Set Random Seed from the popup menu on the Augment Design title bar. A dialog shows the most recently used random number. Click OK to use that number again, or Cancel to generate a design based on a new random number. The dialog in Specifying a Random Number shows the random number (12834729) used to generate the runs in D-Optimally Augmented Factor Settings.
|
7.
|
Suppose you have already run the experiment on the augmented data and recorded results in the Percent Reacted column of the data table.
|
1.
|
To see these results, open Reactor Augment Data.jmp found in the Design Experiment sample data folder installed with JMP.
|
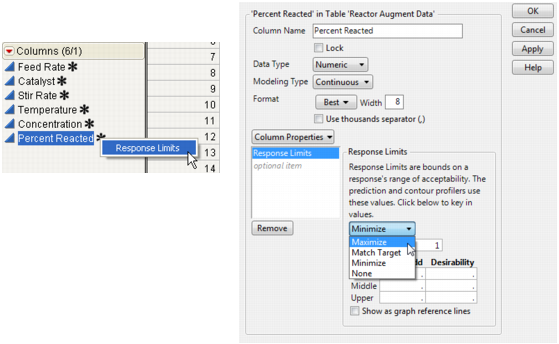
It is desirable to maximize Percent Reacted. However, the column’s Response Limits column property in this sample data table is set to Minimize.
|
2.
|
Click the asterisk next to the Percent Reacted column name in the Columns panel of the data table and select Response Limits, as shown on the left in Change the Response Limits Column Property for the Percent Reacted Column.
|
|
3.
|
In the Column Info dialog that appears, change the response limit to Maximize, as shown on the right in Change the Response Limits Column Property for the Percent Reacted Column.
|
|
4.
|
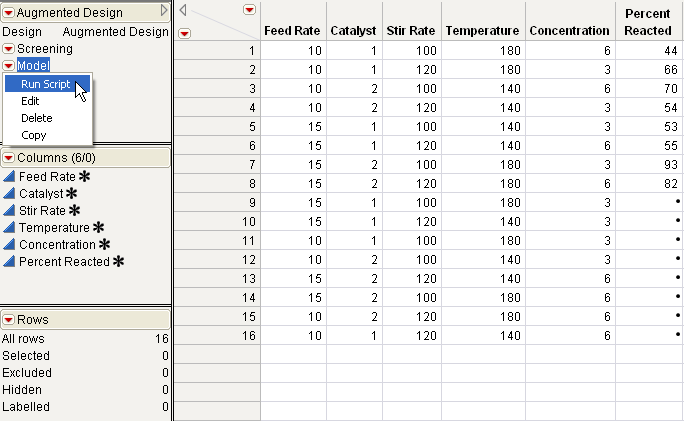
To start the analysis, select Run Script from the Model red triangle menu in the upper left corner of the data table (Completed Augmented Experiment (Reactor Augment Data.jmp)).
|
The Model script, stored as a table property with the data, contains the JSL commands that display the Fit Model dialog with all main effects and two-factor interactions as effects.
|
5.
|
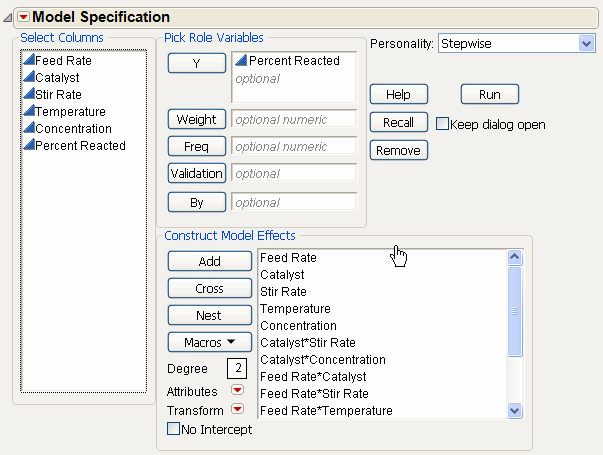
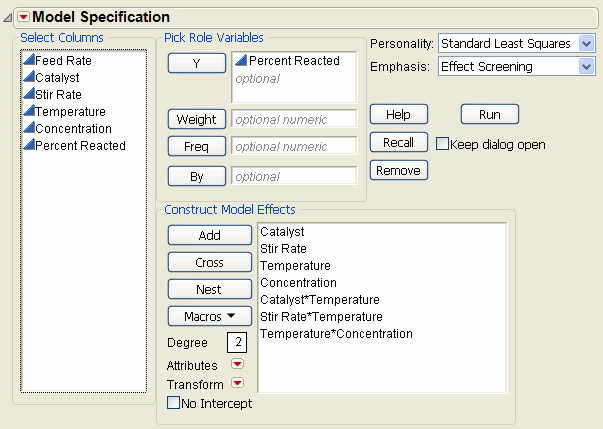
Change the fitting personality on the Fit Model dialog from Standard Least Squares to Stepwise, as shown in Fit Model Dialog for Stepwise Regression on Generated Model.
|
|
6.
|
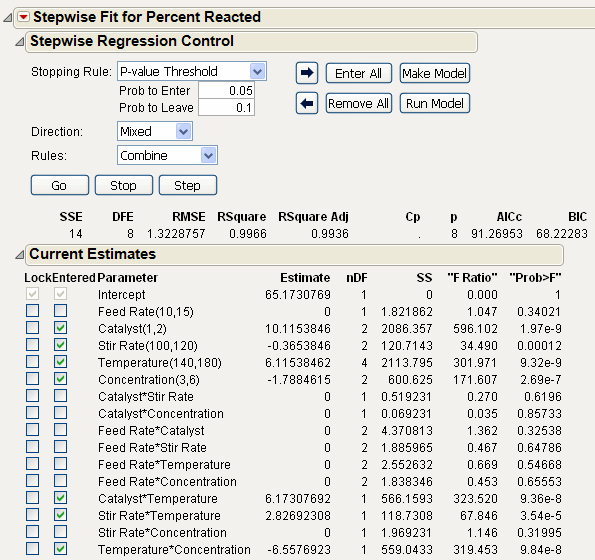
When you click Run, the stepwise regression control panel appears. Click the check boxes for all the main effect terms.
|
Note: Select P-value Threshold from the Stopping Rule menu, Mixed from the Direction menu, and make sure Prob to Enter is 0.050 and Prob to Leave is 0.100. These are not the default values. Follow the dialog shown in Initial Stepwise Model.
|
7.
|
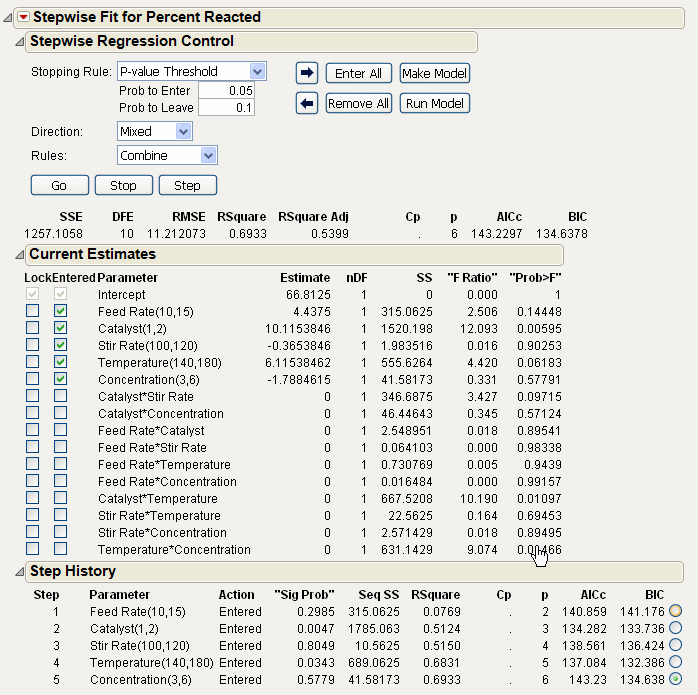
Click Go to start the stepwise regression. The process continues until all terms are entered into the model that meet the Prob to Enter and Prob to Leave criteria in the Stepwise Regression Control panel.
|
Completed Stepwise Model shows the result of this example analysis. Note that Feed Rate is out of the model while the Catalyst*Temperature, Stir Rate*Temperature, and the Temperature*Concentration interactions have entered the model.
|
8.
|
After Stepwise is finished, click Make Model on the Stepwise control panel to generate this reduced model, as shown in New Prediction Model Dialog.
|
|
9.
|
Click Run and fit the reduced model to do additional diagnostic work, make predictions, and find the optimal factor settings.
|
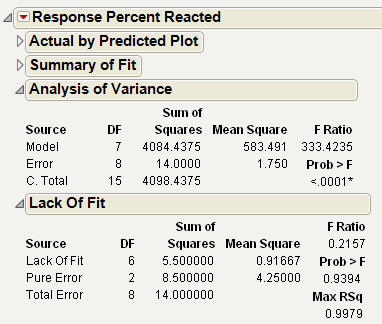
The Analysis of Variance and Lack of Fit Tests in Prediction Model Analysis of Variance and Lack of Fit Tests, indicate a highly significant regression model with no evidence of Lack of Fit.
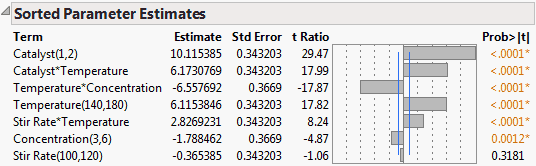
The Sorted Parameter Estimates table in Prediction Model Estimates Plot shows that Catalyst has the largest main effect. However, the significance of the two-factor interactions is of the same order of magnitude as the main effects. For this reason, the initial screening experiment in A Standard Design for Five Continuous Factors in Screening Designs had ambiguous results.
|
10.
|
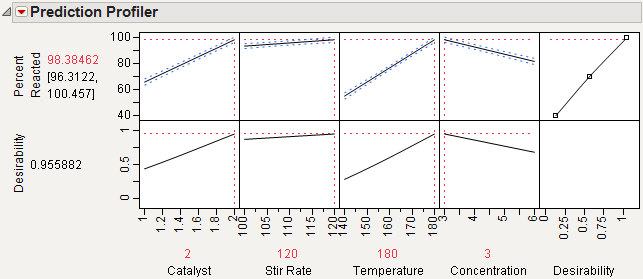
Choose Maximize Desirability from the menu on the Prediction Profiler title bar.
|
The prediction profile plot in Maximum Percent Reacted shows that maximum occurs at the high levels of Catalyst, Stir Rate, and Temperature and the low level of Concentration. At these extreme settings, the estimate of Percent Reacted increases from 65.17 to 98.38.
|
•
|
In A Standard Design with Two Continuous Factors and One Categorical Factor in Screening Designs, a screening design with only 8 runs was analyzed. The analysis produced a model with the five main effects and two interaction effects with confounding. None of the factors effects were significant, although the Catalyst factor was large enough to encourage collecting data for further runs.
|
|
•
|
In The Five-Factor Reactor Example, a full factorial of the five two-level reactor factors, 32 runs, was first subjected to a stepwise regression. This approach identified three main effects (Catalyst, Temperature, and Concentration) and two interactions (Temperature*Catalyst, Concentration*Temperature) as significant effects.
|