The Fit Line command finds the parameters 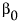 and
and 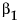 for the straight line that fits the points to minimize the residual sum of squares. The model for the ith row is written
for the straight line that fits the points to minimize the residual sum of squares. The model for the ith row is written 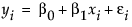 .
.
A polynomial of degree 2 is a parabola; a polynomial of degree 3 is a cubic curve. For degree k, the model for the ith observation is as follows:
Standard least square fitting assumes that the X variable is fixed and the Y variable is a function of X plus error. If there is random variation in the measurement of X, you should fit a line that minimizes the sum of the squared perpendicular differences. See Line Perpendicular to the Line of Fit. However, the perpendicular distance depends on how X and Y are scaled, and the scaling for the perpendicular is reserved as a statistical issue, not a graphical one.
The fit requires that you specify the ratio of the variance of the error in Y to the error in X. This is the variance of the error, not the variance of the sample points, so you must choose carefully. The ratio 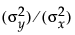 is infinite in standard least squares because
is infinite in standard least squares because 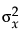 is zero. If you do an orthogonal fit with a large error ratio, the fitted line approaches the standard least squares line of fit. If you specify a ratio of zero, the fit is equivalent to the regression of X on Y, instead of Y on X.
is zero. If you do an orthogonal fit with a large error ratio, the fitted line approaches the standard least squares line of fit. If you specify a ratio of zero, the fit is equivalent to the regression of X on Y, instead of Y on X.
The most common use of this technique is in comparing two measurement systems that both have errors in measuring the same value. Thus, the Y response error and the X measurement error are both the same type of measurement error. Where do you get the measurement error variances? You cannot get them from bivariate data because you cannot tell which measurement system produces what proportion of the error. So, you either must blindly assume some ratio like 1, or you must rely on separate repeated measurements of the same unit by the two measurement systems.
An advantage to this approach is that the computations give you predicted values for both Y and X; the predicted values are the point on the line that is closest to the data point, where closeness is relative to the variance ratio.
Using quantities from the corresponding analysis of variance table, the Rsquare for any continuous response fit is calculated as follows:
The mean square for Error is in the Analysis of Variance report. See Examples of Analysis of Variance Reports for Linear and Polynomial Fits. You can compute the mean square for C. Total as the Sum of Squares for C. Total divided by its respective degrees of freedom.
For the Pure Error DF, consider the multiple instances in the Big Class.jmp sample data table where more than one subject has the same value of height. In general, if there are g groups having multiple rows with identical values for each effect, the pooled DF, denoted DFp, is as follows:
For the Pure Error SS, in general, if there are g groups having multiple rows with the same x value, the pooled SS, denoted SSp, is written as follows:
Because Pure Error is invariant to the form of the model and is the minimum possible variance, Max RSq is calculated as follows:
Std Beta is calculated as follows:
Design Std Error is calculated as the standard error of the parameter estimate divided by the RMSE.
R-Square is equal to 1-(SSE/C.Total SS), where C.Total SS is available in the Fit Line ANOVA report.
The Pearson correlation coefficient is denoted r, and is computed as follows:
Where 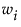 is either the weight of the ith observation if a weight column is specified, or 1 if no weight column is assigned.
is either the weight of the ith observation if a weight column is specified, or 1 if no weight column is assigned.


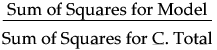


 where
where