The Logistic Report

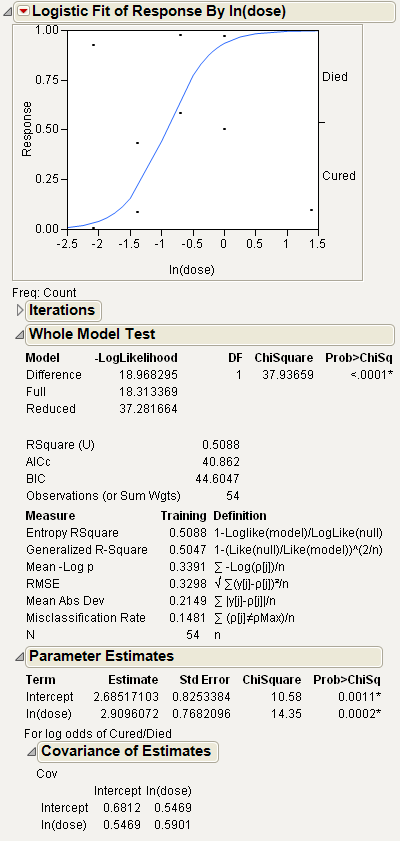
To produce the plot shown in Example of a Logistic Report, follow the instructions in Example of Nominal Logistic Regression.

Example of a Logistic Report

The Logistic report window contains the Logistic plot, the Iterations report, the Whole Model Test report, and the Parameter Estimates report.

Note: The red triangle menu provides more options that can add to the initial report window. See Logistic Platform Options.

Logistic Plot

The logistic probability plot gives a complete picture of what the logistic model is fitting. At each x value, the probability scale in the y direction is divided up (partitioned) into probabilities for each response category. The probabilities are measured as the vertical distance between the curves, with the total across all Y category probabilities summing to 1.

Replace variables in the plot in one of two ways: swap existing variables by dragging and dropping a variable from one axis to the other axis; or, click on a variable in the Columns panel of the associated data table and drag it onto an axis.

Related Information

•	Additional Example of a Logistic Plot

Iterations

The Iterations report shows each iteration and the evaluated criteria that determine whether the model has converged. Iterations appear only for nominal logistic regression.

Whole Model Test

The Whole Model Test report shows if the model fits better than constant response probabilities. This report is analogous to the Analysis of Variance report for a continuous response model. It is a specific likelihood-ratio Chi-square test that evaluates how well the categorical model fits the data. The negative sum of natural logs of the observed probabilities is called the negative log-likelihood (–LogLikelihood). The negative log-likelihood for categorical data plays the same role as sums of squares in continuous data. Twice the difference in the negative log-likelihood from the model fitted by the data and the model with equal probabilities is a Chi-square statistic. This test statistic examines the hypothesis that the x variable has no effect on the responses.

Values of the Rsquare (U) (sometimes denoted as R2) range from 0 to 1. High R2 values are indicative of a good model fit, and are rare in categorical models.

Description of the Whole Model Test

Model

(sometimes called Source)

•	The Reduced model only contains an intercept.

•	The Full model contains all of the effects as well as the intercept.

•	The Difference is the difference of the log likelihoods of the full and reduced models.

Records the degrees of freedom associated with the model.

–LogLikelihood

Measures variation, sometimes called uncertainty, in the sample.

Full (the full model) is the negative log-likelihood (or uncertainty) calculated after fitting the model. The fitting process involves predicting response rates with a linear model and a logistic response function. This value is minimized by the fitting process.

Reduced (the reduced model) is the negative log-likelihood (or uncertainty) for the case when the probabilities are estimated by fixed background rates. This is the background uncertainty when the model has no effects.

The difference of these two negative log-likelihoods is the reduction due to fitting the model. Two times this value is the likelihood-ratio Chi-square test statistic.

For more information, see Fitting Linear Models.

Chi-Square

The likelihood-ratio Chi-square test of the hypothesis that the model fits no better than fixed response rates across the whole sample. It is twice the –LogLikelihood for the Difference Model. It is two times the difference of two negative log-likelihoods, one with whole-population response probabilities and one with each-population response rates.

For more information, see Statistical Details for the Whole Model Test Report.

Prob>ChiSq

The observed significance probability, often called the p value, for the Chi-square test. It is the probability of getting, by chance alone, a Chi-square value greater than the one computed. Models are often judged significant if this probability is below 0.05.

Rsquare (U)

The proportion of the total uncertainty that is attributed to the model fit.

To test that the factor variable has no effect on the response, look at the difference between the following:

•	the log-likelihood from the fitted model

•	the log-likelihood from the model that uses horizontal lines

For more information, see Statistical Details for the Whole Model Test Report.

AICc

The corrected Akaike Information Criterion. See Fitting Linear Models.

BIC

The Bayesian Information Criterion. See Fitting Linear Models.

Observations

(sometimes called Sum Wgts)

The total sample size used in computations. If you specified a Weight variable, this is the sum of the weights.

Measure

The available measures of fit are as follows:

Entropy RSquare

compares the log-likelihoods from the fitted model and the constant probability model.

Generalized RSquare

is a measure that can be applied to general regression models. It is based on the likelihood function L and is scaled to have a maximum value of 1. The Generalized RSquare measure simplifies to the traditional RSquare for continuous normal responses in the standard least squares setting. Generalized RSquare is also known as the Nagelkerke or Craig and Uhler R2, which is a normalized version of Cox and Snell’s pseudo R2. See Nagelkerke (1991).

Mean -Log p

is the average of -log(p), where p is the fitted probability associated with the event that occurred.

RMSE

is the root mean square error, where the differences are between the response and p (the fitted probability for the event that actually occurred).

Mean Abs Dev

is the average of the absolute values of the differences between the response and p (the fitted probability for the event that actually occurred).

Misclassification Rate

is the rate for which the response category with the highest fitted probability is not the observed category.

For Entropy RSquare and Generalized RSquare, values closer to 1 indicate a better fit. For Mean -Log p, RMSE, Mean Abs Dev, and Misclassification Rate, smaller values indicate a better fit.

Training

The value of the measure of fit.

Definition

The algebraic definition of the measure of fit.

Parameter Estimates

The nominal logistic model fits a parameter for the intercept and slope for each of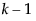

logistic comparisons, where k is the number of response levels. The Parameter Estimates report lists these estimates. Each parameter estimate can be examined and tested individually, although this is seldom of much interest.

Description of the Parameter Estimates Report
Term	Lists each parameter in the logistic model. There is an intercept and a slope term for the factor at each level of the response variable, except the last level.
Estimate	Lists the parameter estimates given by the logistic model.
Std Error	Lists the standard error of each parameter estimate. They are used to compute the statistical tests that compare each term to zero.
Chi-Square	Lists the Wald tests for the hypotheses that each of the parameters is zero. The Wald Chi-square is computed as (Estimate/Std Error)2.
Prob>ChiSq	Lists the observed significance probabilities for the Chi-square tests.

Covariance of Estimates

Reports the estimated variances of the parameter estimates, and the estimated covariances between the parameter estimates. The square root of the variance estimates is the same as those given in the Std Error section.