Design That Avoids Aliasing of Main Effects and Two-Factor Interactions
Suppose that your primary interest is in estimating the main effects of six continuous factors. However, you want to do this in a way that minimizes aliasing of main effects with potentially active two-factor interactions.
Your budget allows for only 16 runs. With six factors, there are 15 possible two-factor interactions. The minimum number of runs required to fit the constant, the six main effects, and the 15 two-factor interactions is 22.
In this example, you find a compromise between an 8-run main effects only design (see Design That Estimates Main Effects Only) and a 22-run design capable of fitting all the two-factor interactions. You use Alias Optimality as the optimality criterion to achieve your goal.
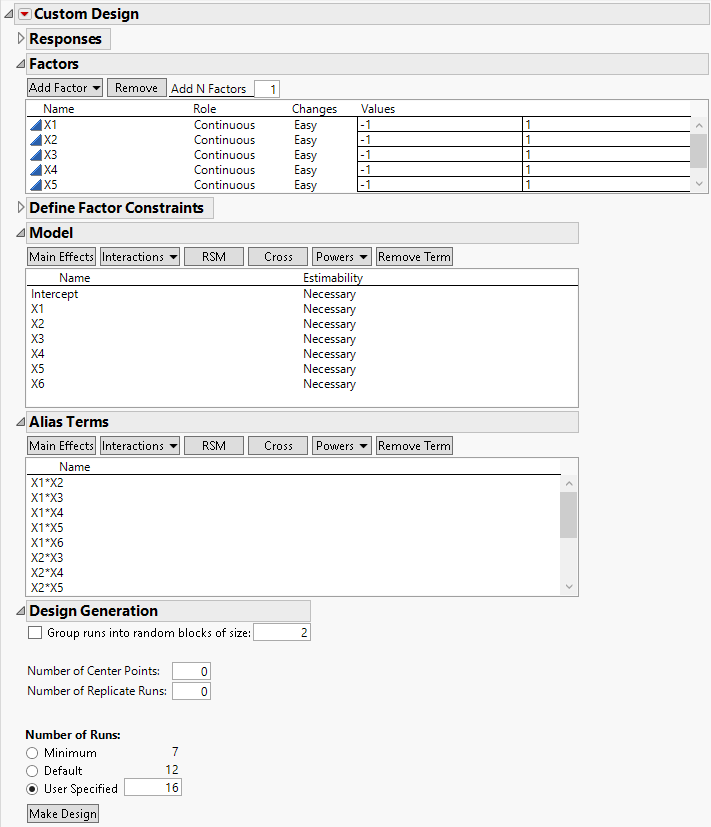
1. Select DOE > Custom Design.
2. Type 6 next to Add N Factors.
3. Click Add Factor > Continuous.
4. Click Continue.
The model includes the main effect terms by default. The default estimability of these terms is Necessary. In the Alias Terms outline, notice that second-order interactions are added. By default, all two-way interactions not included in the assumed model are added to the Alias Terms list.
5. Click the Custom Design red triangle and select Optimality Criterion > Make Alias Optimal Design.
The Make Alias Optimal Design selection tells JMP to generate a design that balances reduction in aliasing with D-efficiency. See Alias Optimality in the Custom Designs section.
6. Click User Specified and change the number of runs to 16.
Figure 5.9 Factors, Model, Alias Terms, and Number of Runs
Note: Setting the Random Seed in step 7 and Number of Starts in step 8 reproduces the exact results shown in this example. In constructing a design on your own, these steps are not necessary.
7. (Optional) Click the Custom Design red triangle, select Set Random Seed, type 12345, and click OK.
8. (Optional) Click the Custom Design red triangle, select Number of Starts, type 10, and click OK.
9. Click Make Design.
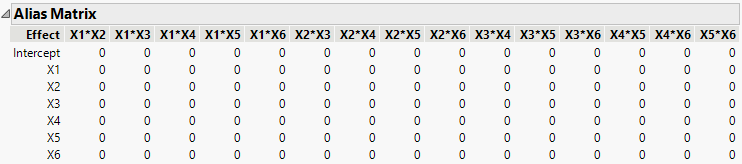
10. Open the Design Evaluation > Alias Matrix outline.
Figure 5.10 Alias Matrix
All rows contain only zeros, which means that the Intercept and main effect terms are not biased by any two-factor interactions.
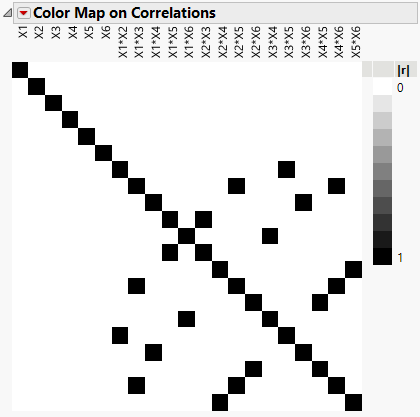
11. Open the Design Evaluation > Color Map on Correlations outline.
Figure 5.11 Color Map on Correlations
The Color Map on Correlations shows that main effects can be estimated independently of two-way interactions. However, some two-way interactions are fully aliased with other two-way interactions. Place your cursor over the off-diagonal red squares to see which two-way interactions are confounded.
It turns out that this particular design is a resolution IV orthogonal screening design. Main effects are not aliased with each other or with two-way interactions. But two-way interactions are fully aliased with other two-way interactions.