Publication date: 04/30/2021
Space-Filling Designs
Space-filling designs are useful in situations where run-to-run variability is of far less concern than the form of the model. Consider a sensitivity study of a computer simulation model. In this situation, and for any mechanistic or deterministic modeling problem, any variability is small enough to be ignored. For systems with no variability, replication, randomization, and blocking are irrelevant.
The Space Filling platform provides designs for situations with both continuous and categorical factors. For continuous factors, space-filling designs have two objectives:
• maximize the distance between any two design points
• space the points uniformly
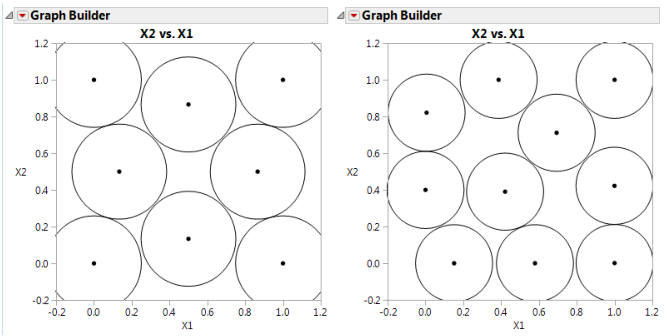
Figure 21.1 Space-Filling Design
Contents
Overview of Space-Filling Designs
Space Filling Design Window
Responses
Factors
Define Factor Constraints
Space Filling Design Methods
Design
Design Diagnostics
Design Table
Space Filling Design Options
Sphere-Packing Designs
Creating a Sphere-Packing Design
Visualizing the Sphere-Packing Design
Latin Hypercube Designs
Creating a Latin Hypercube Design
Visualizing the Latin Hypercube Design
Uniform Designs
Comparing Sphere-Packing, Latin Hypercube, and Uniform Methods
Minimum Potential Designs
Maximum Entropy Designs
Gaussian Process IMSE Optimal Designs
Fast Flexible Filling Designs
FFF Optimality Criterion
Set Average Cluster Size
Constraints
Creating and Viewing a Constrained Fast Flexible Filling Design
Creating a Space-Filling Design for a Map Shape
Example of a Sphere-Packing Design
Create the Sphere-Packing Design for the Borehole Data
Guidelines for the Analysis of Deterministic Data
Want more information? Have questions? Get answers in the JMP User Community (community.jmp.com).