Special Reports
This section describes the reports that are available based on the data structure or choices that you made regarding effect attributes.
Singularity Details
When there are linear dependencies among model effects, the Singularity Details report appears as the first report under the Response report title. It contains a table of the linear functions that the model terms satisfy. These functions define the aliasing relationships among model terms. Figure 3.7 shows an example for the Singularity.jmp sample data table.
Figure 3.7 Singularity Details Report
When there are linear dependencies among effects, estimates of some model terms are not unique. See Models with Linear Dependencies among Model Terms.
Response Surface Report
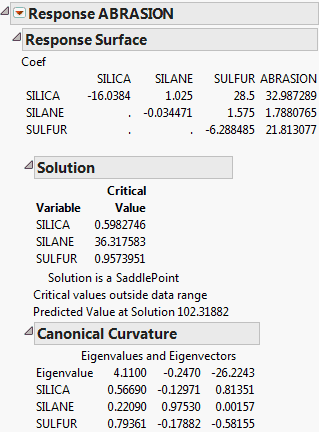
When an effect in a model has the response surface (&RS) or mixture response surface (&RS&Mixture) attribute, a Response Surface report is provided. See Figure 3.8 for an example of a Response Surface report for the Tiretread.jmp sample data table.
Figure 3.8 Response Surface Report
Coef Table
The Coef table shown as the first part of the Response Surface report gives a concise summary of the estimated model parameters. The first columns give the coefficients of the second-order terms. The last column gives the coefficients of the linear terms. To see the prediction expression in its entirety, select Estimates > Show Prediction Expression from the report’s red triangle menu.
Solution Report
The Solution report gives a critical value (maximum, minimum, or saddle point), if one exists, along with the predicted value at that point. It also alerts you if the solution falls outside the range of the data.
Canonical Curvature Report
The eigenvalues and eigenvectors of the matrix of second-order parameter estimates determine the type of curvature. The eigenvectors show the principal directions of the surface, including the directions of greatest and smallest curvature.
The eigenvalues are provided in the first row of the Canonical Curvature table.
• If the eigenvalues are negative, the response surface curves downward from a maximum.
• If the eigenvalues are positive, the surface shape curves upward from a minimum.
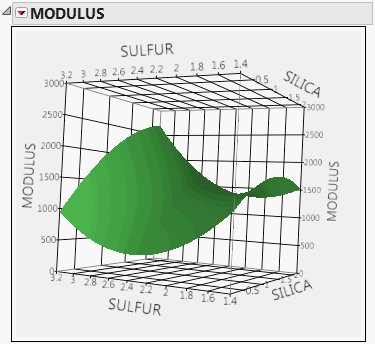
• If there are both positive and negative eigenvalues, the surface is saddle shaped, curving up in one direction and down in another direction. See Figure 3.9 for an example using the Tiretread.jmp sample data table.
Figure 3.9 Surface Profiler Plot with Saddle-Shaped Surface
The eigenvectors listed below the eigenvalues show the orientation of the principal axes. The larger the absolute value of an eigenvalue, the greater the curvature of the response surface in its associated direction. Sometimes a zero eigenvalue occurs. This eigenvalue means that, along the direction described by the corresponding eigenvector, the fitted surface is flat.
Note: The response surface report is not shown for response surface models consisting of more than 20 factors. No error message or alert is given. For more information about response surface designs, see Response Surface Designs in the Design of Experiments Guide.
Mixed and Random Effect Model Reports
When you specify a random effect in the Fit Model launch window, the Method list appears. This list provides two fitting methods: REML (Recommended) and EMS (Traditional). Additional reports as well as Save Columns and Profiler options are shown, based on the model and the method that you select.
For more information about the REML method reports, see Restricted Maximum Likelihood (REML) Method. For more information about the EMS method reports, see EMS (Traditional) Model Fit Reports.
Crossvalidation Report
 When you enter a Validation column in the Fit Model launch window, a Crossvalidation report is provided. The report gives the following for each of the sets used in validation:
When you enter a Validation column in the Fit Model launch window, a Crossvalidation report is provided. The report gives the following for each of the sets used in validation:
Source
Identifies the set as the Training, Validation, or Test set.
RSquare
The RSquare value calculated for observations in the given set relative to the model derived using the Training Set. For the Training Set, this is the usual RSquare value.
For each of the Training, Validation, and Test sets, the RSquare value is computed as follows:
– For each observation in the given set, compute the prediction error. This is the difference between the actual response and the response predicted by the Training set model.
– Square and sum the prediction errors to obtain SSESource, where the subscript Source denotes any of the Training, Validation, or Test sets.
– Square and sum the differences between the actual responses for observations in the Source set and their mean. Denote this value by SSTSource.
– RSquare for the Source set is:
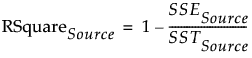
Note: It is possible for RSquare values for the Validation and Test sets to be negative.
RASE
The square root of the mean squared prediction error. For each of the Training, Validation, and Test sets, RASE is computed as follows:
– For each observation in the given set, calculate the prediction error. This is the difference between the actual response and the response predicted by the Training set model.
– Square and sum the prediction errors to obtain SSESource, where the subscript Source denotes any of the Training, Validation, or Test sets.
– Denote the number of observations by n.
– RASE is:
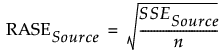
Note: In the Stepwise Fit report, the RASE values for the Validation and Test sets are called RMSE Validation and RMSE Test. See RMSE Validation in the Stepwise Regression Models section.
Freq
The number of observations in the Source set.