Use Regression with Multiple Predictors
The section Use Regression with One Predictor showed you how to build simple regression models consisting of one predictor variable and one response variable. Multiple regression predicts the average response variable using two or more predictor variables.
Scenario
This example uses the Candy Bars.jmp data table, which contains nutrition information for candy bars.
A dietitian wants to predict calories using the following information:
• Total fat
• Carbohydrates
• Protein
Use multiple regression to predict the average response variable using these three predictor variables.
Discover the Relationship
To visualize the relationship between calories and total fat, carbohydrates, and protein, create a scatterplot matrix:
1. Select Help > Sample Data Library and open Candy Bars.jmp.
2. Select Graph > Scatterplot Matrix.
3. Select Calories and click Y, Columns.
4. Select Total fat g, Carbohydrate g, and Protein g, and click X.
5. Click OK.
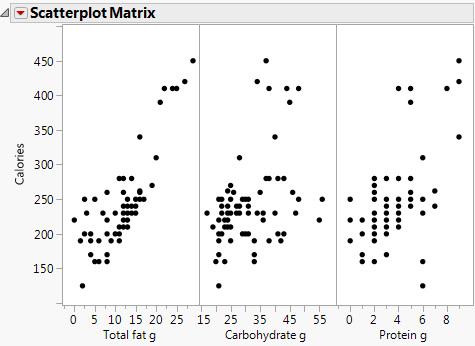
Figure 5.26 Scatterplot Matrix Results
The scatterplot matrix shows that there is a positive correlation between calories and all three variables. The correlation between calories and total fat is the strongest. Now that the dietitian knows that there is a relationship, the dietitian can build a multiple regression model to predict average calories.
Build the Multiple Regression Model
Continue to use the Candy Bars.jmp sample data table.
1. Select Analyze > Fit Model.
2. Select Calories and click Y.
3. Select Total Fat g, Carbohydrate g, and Protein g and click Add.
4. Next to Emphasis, select Effect Screening.
Figure 5.27 Fit Model Window
5. Click Run.
The report window shows the model results. To interpret the model results, focus on these areas:
• View the Actual by Predicted Plot
• Interpret the Parameter Estimates
Note: For more information about all of the model results, see Model Specification in Fitting Linear Models.
View the Actual by Predicted Plot
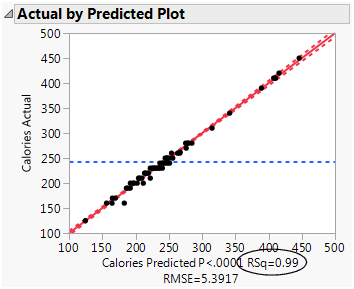
The Actual by Predicted Plot shows the actual calories versus the predicted calories. As the predicted values come closer to the actual values, the points on the scatterplot fall closer around the red line (Figure 5.28). Because the points are all very close to the line, you can see that the model predicts calories based on the chosen factors well.
Figure 5.28 Actual by Predicted Plot
Another measure of model accuracy is the RSq value (which appears below the plot in Figure 5.28). The RSq value measures the percentage of variability in calories, as explained by the model. A value closer to 1 means a model is predicting well. In this example, the RSq value is 0.99.
Interpret the Parameter Estimates
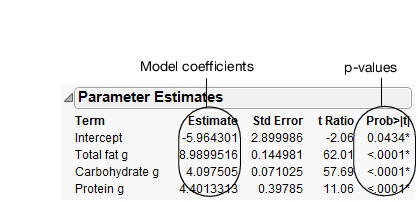
The Parameter Estimates report shows the following information:
• The model coefficients
• p-values for each parameter
Figure 5.29 Parameter Estimates Report
In this example, the p-values are all very small (<.0001). This indicates that all three effects (fat, carbohydrate, and protein) contribute significantly when predicting calories.
You can use the model coefficients to predict the value of calories for particular values of fat, carbohydrate, and protein. For example, suppose that you want to predict the average calories for any candy bar that has these characteristics:
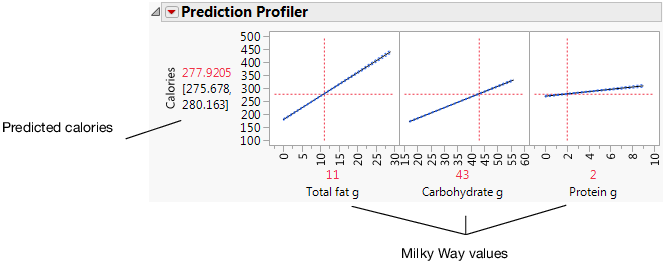
• Fat = 11 g
• Carbohydrate = 43 g
• Protein = 2 g
Using these values, you can calculate the predicted average calories as follows:
277.92 = -5.9643 + 8.99*11 + 4.0975*43 + 4.4013*2
The characteristics in this example are the same as the Milky Way candy bar (on row 59 of the data table). The actual calories for the Milky Way are 280, showing that the model predicts well.
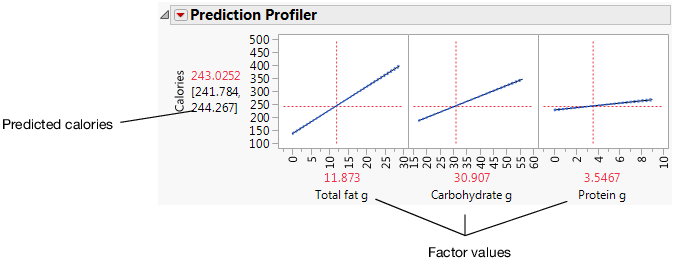
Use the Prediction Profiler
Use the Prediction Profiler to see how changes in the factors affect the predicted values. The profile lines show the magnitude of change in calories as the factor changes. The line for Total fat g is the steepest, meaning that changes in total fat have the largest effect on calories.
Figure 5.30 Prediction Profiler
Click and drag the vertical line for each factor to see how the predicted value changes. You can also click the current factor values and change them. For example, click the factor values and type the values for the Milky Way candy bar (row 59).
Figure 5.31 Factor Values for the Milky Way
Note: For more information about the Prediction Profiler, see Profiler in Profilers.
Draw Conclusions
The dietitian now has a good model to predict calories of a candy bar based on its total fat, carbohydrates, and protein.