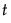ここでは、[スコアオプション]>[計算式の保存]で保存される計算式について説明します。計算式は判別法によって異なります。
カテゴリカル変数Xによって定義される各グループについて、共変量のオブザベーションは、p次(pは共変量の数)の多変量正規分布に従うと仮定されます。計算式で使用される記号は、[計算式の保存]で保存される計算式の記号のとおりです。
|
nt
|
グループt内のオブザベーション数
|
|
ybar
|
|
|
qt
|
グループtに属する事前確率
|
|
yがグループtに属する事後確率
|
|
|
|A|
|
線形判別法では、「群内共分散行列はすべてのグループで等しい」と仮定されます。この共通した共分散行列は、Spと推定されます。以下の式で用いている記号については、[計算式の保存]で保存される計算式の記号を参照してください。
推定されるパラメータの個数は、プールした共分散行列におけるp(p+1)/2個と、平均ベクトルにおけるTp個です。よって、線形判別分析において推定されるパラメータの総数は、p(p+1)/2 + Tp個です。
グループtに属する事後確率は、次のように求められます。
オブザベーションyは、事後確率の値が最も大きいグループに割り当てられます。
|
SqDist[<group t>]
|
|
|
Prob[<group t>]
|
|
|
Pred <X>
|
2次判別法では、「グループごとに群内共分散行列が異なる」と仮定されます。グループtにおける群内共分散行列は、Stと推定されます。 つまり、推定されるパラメータの個数は、群内共分散行列におけるTp(p+1)/2個と、平均ベクトルにおけるTp個です。よって、2次判別分析において推定されるパラメータの総数は、Tp(p+3)/2個です。
グループの標本サイズがpと比べて小さい場合、群内共分散行列の推定値はかなり不安定になります。そして、判別スコアは、群内共分散行列の逆行列における最小固有値から大きな影響を受けます。Friedman(1989)を参照してください。そのため、グループの標本サイズがpに比べて小さい場合は、第 “正則化判別法”で説明されている正則化判別法を用いることを検討してください。
グループtに属する事後確率は、次のように求められます。
オブザベーションyは、事後確率の値が最も大きいグループに割り当てられます。
|
SqDist[<group t>]
|
|
|
Prob[<group t>]
|
|
|
Pred <X>
|
|
•
|
パラメータλは、プールして計算された群内共分散行列と、(グループごとに異なると仮定されて)各グループごとに計算された群内共分散行列との重みのバランスを取ります。
|
|
•
|
パラメータγは、対角行列への縮小の度合いを決定します。
|
正則化判別法では、上記した2つの正則化によって、2次判別分析の推定結果を安定させます。Friedman(1989)を参照してください。以下の式で用いている記号については、[計算式の保存]で保存される計算式の記号を参照してください。
正則化判別法の場合、グループtの共分散行列は次のように求められます。
グループtに属する事後確率は、次のように求められます。
オブザベーションyは、事後確率の値が最も大きいグループに割り当てられます。
|
SqDist[<group t>]
|
|
|
Prob[<group t>]
|
|
|
Pred <X>
|
[線形 横長データ]オプションによって実行される判別法は、共変量の個数が多い場合、特に、共変量の個数がオブザベーション数より多い場合(p > n)に役立ちます。この手法では、プールした群内共分散行列Spの逆行列やその転置行列を、p > nの場合に計算負荷がない方式で計算します。特異値分解によって、大規模な共分散行列の逆行列を計算することを回避します。
以下の式で用いている記号については、[計算式の保存]で保存される計算式の記号を参照してください。[線形 横長データ]の判別法は、以下の手順で算出されています。
|
1.
|
|
2.
|
|
3.
|
|
5.
|
|
6.
|
|
7.
|
Ysを特異値分解します。
|
Rは次のように表せます。
|
8.
|
Rがフルランクではない場合、Rの疑似逆行列は次のように定義されます。
これにより、Rの平方根の逆数に相当する行列を、次のように定義します。
|
9.
|
計算式を保存すると、Mahalanobisの距離は分解によって求められます。オブザベーションyのグループtまでの距離は、次のようにして求められます。最後の等式におけるSqDist[0]と Discrim Prin Comp(「判別主成分」)は、第 “保存される計算式”で定義されているものです。
|
SqDist[<group t>]
|
|
|
Prob[<group t>]
|
|
|
Pred <X>
|
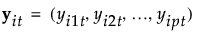
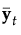
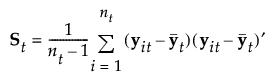
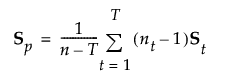
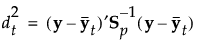
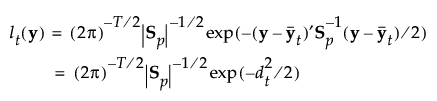
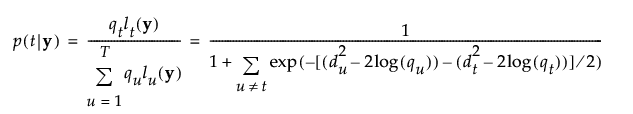
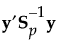
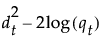
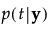
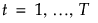 に関して、
に関して、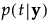 が最大となるような
が最大となるような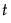
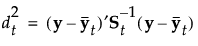
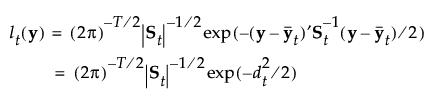
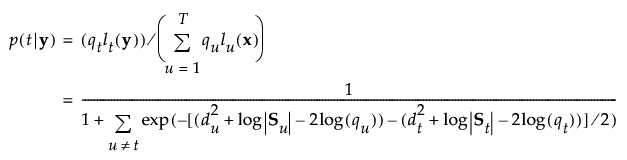
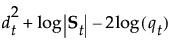
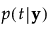
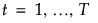 に関して、
に関して、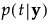 が最大となるような
が最大となるような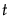
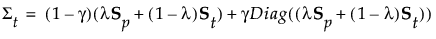
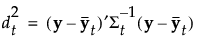
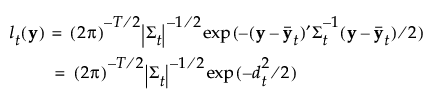
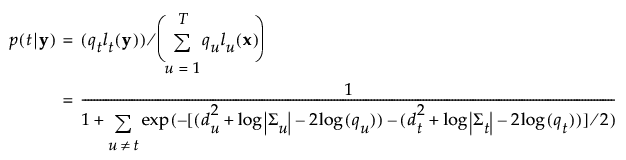
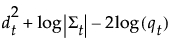
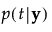
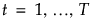 に関して、
に関して、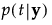 が最大となるような
が最大となるような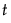
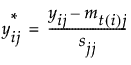
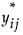 の値の行列を
の値の行列を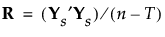
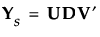
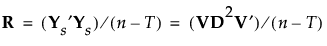
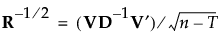
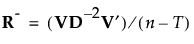
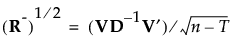
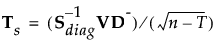
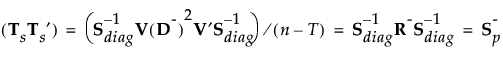
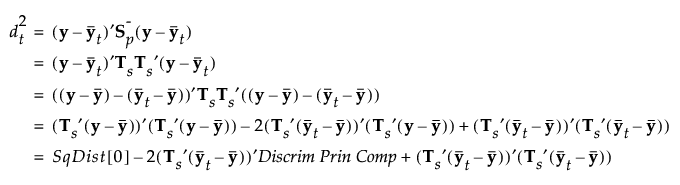
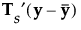 によって求められます。この式で、
によって求められます。この式で、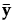 は、全体平均を表す
は、全体平均を表す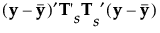
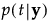 。
。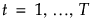 に関して、
に関して、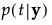 が最大となるような
が最大となるような