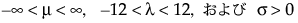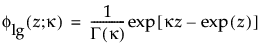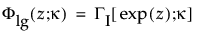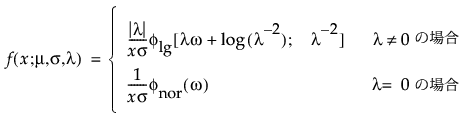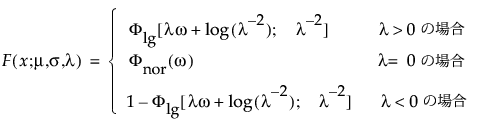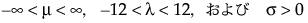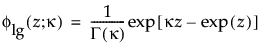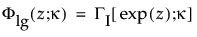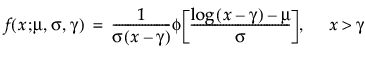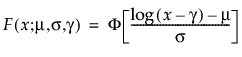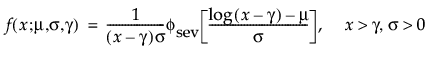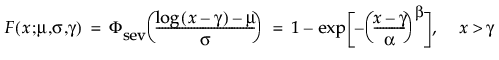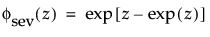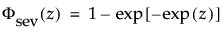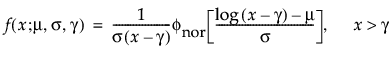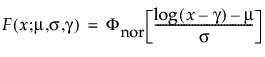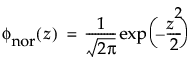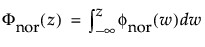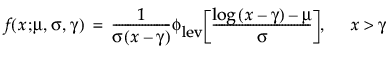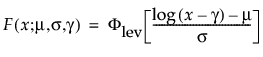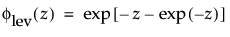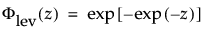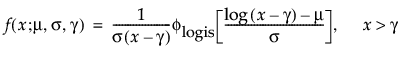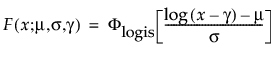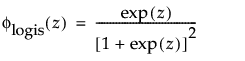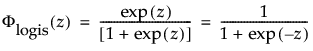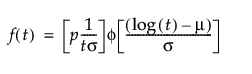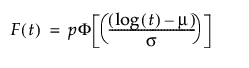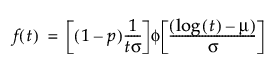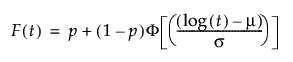ここでは、「寿命の一変量」で用意されている確率分布や計算の詳細を説明します。理論や応用、そして以下で紹介するノンパラメトリックおよびパラメトリックな推定については、Meeker and Escobar(1998, ch. 2-5)に優れた説明があります。
閾値パラメータをもつ分布以外は、最尤法で推定されます。閾値パラメータをもつ分布で、 最小の観測値が、打ち切りデータではなく、厳密な故障時間を示す値であった場合、ごく短い区間に含まれる区間打ち切りデータとして、その最小の観測値を処理します。そして、このような微調整をした後、最尤法を適用します。このような微調整をしないと、尤度が無限大となり、最尤法が行えない場合があります。このアプローチは、Meeker and Escobar(1998、p. 275)が提唱している方法とほぼ同じです。 ただし、JMPでは、最小の厳密な故障時間だけを区間打ち切りにします。このような微調整をすると、閾値パラメータをもつ分布の尤度関数も、確実に有界になります。
「寿命の一変量」プラットフォームには、分布パラメータの信頼区間を計算する方法が2つ用意されています。「寿命の一変量」プラットフォームの起動ウィンドウで、それぞれ[Wald]または[尤度]を選択することにより、2つの方法のいずれかを選ぶことができます。デフォルトの設定は[Wald]です。累積分布関数の信頼区間は、標準化した変数に対してWald法に基づく信頼区間を計算し、 それを累積分布関数に変換することで算出されます(Nelson, 1982, p. 332-333およびp. 346-347)。そのほかの信頼区間は、(変数変換を伴う)Wald法によって求められています(Meeker and Escobar, 1998, ch. 7)。対数尤度の等高線図には、2パラメータに対する信頼領域が表示されます。この等高線は、尤度比から計算されています(Meeker and Escobar, 1998, ch. 8)。
メモ: JMPでは、多くの確率分布を、位置パラメータと尺度パラメータで表現します。対数正規分布の場合は、メディアン(中央値)もレポートに表示します。また、閾値をもつ分布は、位置と尺度のほかに、閾値パラメータも含んでいます。次節での数式において、位置パラメータをμ、尺度パラメータをσ、閾値パラメータをγと記します。
Weibull分布は、ハザードが時間とともに上昇または低下する故障時間データに適しています。形状パラメータβの値に基づいて、さまざまな種類のデータを非常に柔軟にモデル化できるため、信頼性分析で広く使われています。Weibull分布は、たとえば、電子部品、ローラーベアリング、キャパシタ(コンデンサ)、セラミックなどの故障時間データに使われてきました。尺度パラメータαと形状パラメータβを変更することで、さまざまな形のWeibull分布を作成できます Weibullの確率密度関数と累積分布関数は、次式のとおりです。
αは尺度パラメータ、βは形状パラメータです。Weibull分布は、βの値を変更することにより柔軟に形状が変わり、特にb = 1のときは指数分布になります。このようなパラメータ化のほかにも、多くの文献で使用され、JMPでも採用している方法として、位置パラメータμ、および尺度パラメータσによってWeibull分布を表す方法もあります。これらは次式で簡単にαとβに変換できます。
Weibull分布の確率密度関数と累積分布関数は、 このパラメータ表現においては、位置パラメータμ = log(α)と尺度パラメータσ = 1/βをもつ最小極値分布に対数変換したデータが従うものとして表すことができます。
正規分布は、比較的単純であるため、中心極限定理が適用できる多くの領域で最も広く使われています。しかし、信頼性分析ではほとんど利用されません。故障時間データでも、μ > 0で、かつ、変動係数(σ/μ)が小さい場合には、正規分布があてはまるときもあります。ハザード関数の増加に上限がないことから、摩耗故障のデータに特に適しています。そのようなデータの例としては、白熱電球、トースターの電熱線、ワイヤーの機械的強度などが挙げられます。確率密度関数と累積分布関数は、次式のとおりです。
最小極値分布(SEV分布; Smallest Extreme Value distribution)は、左に歪んでいる非対称な分布です。2つのケースに適しています。1つは、短時間で故障するユニットが少ない(多数の観測値のうちごく少数が左裾にあるような)場合です。もう1つは、μに比べてσが小さいデータです(その場合、最小極値分布でゼロ以下になる確率が小さいため)。最小極値分布は、時間の経過とともにハザードが上昇するデータに適しています。データ例としては、高齢者の死亡率や、干ばつの間の降水量などが挙げられます。この分布は、Gumbel分布と呼ばれることもあります。確率密度関数と累積分布関数は、次式のとおりです。
最大極値分布(LEV分布; Largest Extreme Value distribution)は、右に歪んでいる非対称な分布です。μ>0と比べてσが小さい故障時間データに使える可能性があります。この分布は、信頼性分析では一般的ではありませんが、大規模な洪水や極端な風速など、極端な自然現象の推定に役立ちます。確率密度関数と累積分布関数は、次式のとおりです。
上の式で、θは尺度パラメータ、γは閾値パラメータです。信頼性分析では、γ = 0の1パラメータ指数分布を頻繁に使います。JMPでは、1パラメータ指数分布だけが用意されています。指数分布は、平均寿命をはるかに超えてからも、一定して故障が起こるような部品の故障時間データによくあてはまります。ハザード(瞬間故障率)が一定であり、ユニットの年齢に依存しません。そのため、材質疲労や腐食、短期的摩耗が生じる機械部品の寿命データには適していません。ただし、ある種の頑健な電子部品のデータには適しています。絶縁油と誘電性流体の寿命を記述する例では、効果的に使われています(Nelson, 1990、p. 53)。
は、それぞれ標準対数ガンマ分布の確率密度関数と累積分布関数です。κ > 0は形状パラメータです。
閾値パラメータをもつ分布は、対数-位置-尺度型の分布に、閾値パラメータを加えたものです。Weibull分布などを、閾値パラメータγを追加することで一般化した分布です。閾値パラメータを追加すると、分布の左端がシフトして0から離れます。閾値パラメータは、シフトパラメータ、最小値パラメータとも呼ばれ、すべてのユニットが閾値を超えて生存することから、保証パラメータと呼ばれることもあります。閾値パラメータを追加すると、分布が時間軸上でシフトしますが、分布の形状と広がりは変化しません。このような閾値分布は、中程度もしくは高程度に、分布がシフトしている場合に適しています。閾値パラメータがある対数-位置-尺度型の分布の確率密度関数と累積分布関数は、一般的に、次式のように表わされます。
上の式で、φとΦは、それぞれ、各分布の標準分布における確率密度関数と累積分布関数です。Weibull分布・対数正規分布・Fréchet分布・対数ロジスティック分布の閾値分布は以下のとおりです。上記の確率密度関数と累積分布関数を、各分布のものに置き換えることにより、導出されます。
|
•
|
pは、全体に占める故障部分母集団の割合です
tは寿命(故障時間)です
μおよびσは、位置と尺度を表すパラメータです。元のデータからゼロ値を除外した後、通常の最尤法で推定されます。
DS分布のより詳細な情報については、Tobias and Trindad(2012, p. 321)を参照してください。
ゼロ強調分布(Zero-Inflated distribution; ZI分布)は、t = 0において一定の割合(p)が故障しているデータに使用します。通常の分布で想定されるよりもゼロ時間での故障個数が多いデータに対して、ゼロが発生する確率を追加してモデル化します。「寿命の一変量」プラットフォームでは、[イベントまでの時間]データの最小値がゼロである場合に、 次の4つのゼロ強調分布を使用できます。
pは、ゼロ値の割合です。
tは、寿命(故障時間)です。
μおよびσは、位置と尺度を表すパラメータです。元のデータからゼロ値を除外した後、通常の最尤法で推定されます。
詳細については、Meeker and Escobar(1995, p. 232)を参照してください。そこでは、一般的な混合分布の式が記載されています。Tobias and Trindade(1995)で述べられている計算式において、α = p、Fd(t) = 1、FN(t) = Φ(t)を代入すると、上の式が得られます。
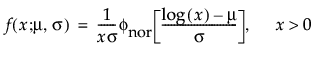
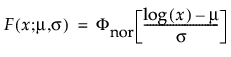 ,
,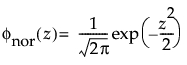
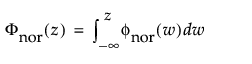
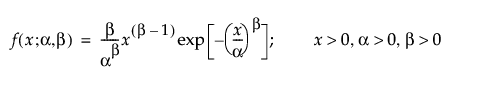
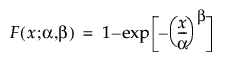 ,
,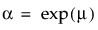
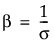
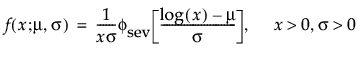
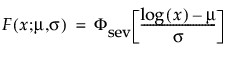
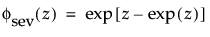
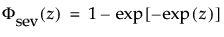
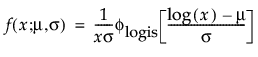
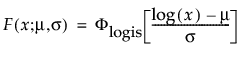 ,
,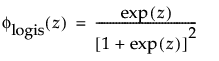
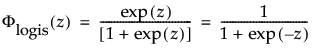
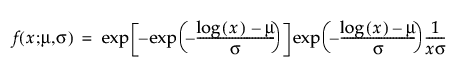
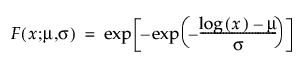
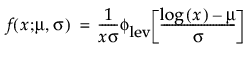
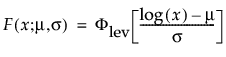
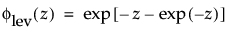
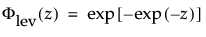
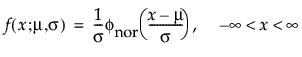
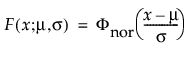
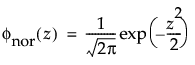
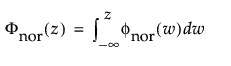
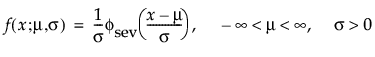
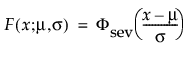
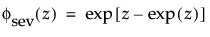
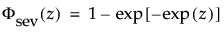
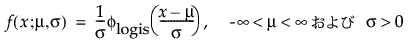
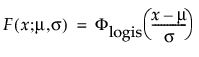
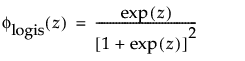
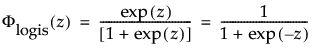
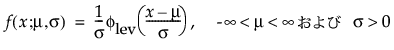
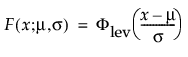
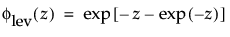
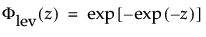
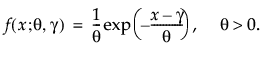
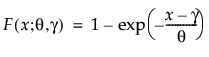
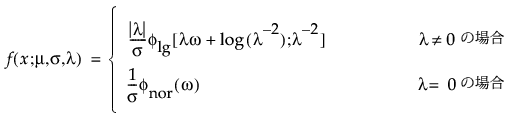
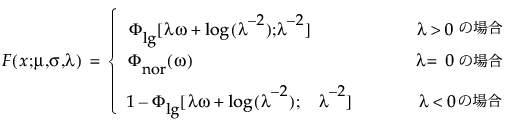
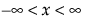 ,
,