検出力分析の例
ここでは、応答変数の「濃度」に対する各効果の影響を検出できるかどうかを調べたいとします。計画には連続尺度の因子が3つ、2水準のカテゴリカル因子が1つ、3水準のカテゴリカル因子が1つ含まれています。3水準のカテゴリカル因子は、元の計画でブロック因子として使用されていたものです。
1. [ヘルプ]>[サンプルデータフォルダ]を選択し、「Design Experiment」フォルダ内の「Coffee Data.jmp」を開きます。
2. [実験計画(DOE)]>[計画の診断]>[計画の評価]を選択します。
3. 「挽き」・「温度」・「時間」・「豆の量」・「場所」を選択し、[X, 説明変数]をクリックします。
「濃度」を[Y, 応答変数]として追加してもかまいませんが、応答を指定してもしなくても、計画の評価結果は同じです。
4. [OK]をクリックします。
5. グレーの開閉アイコンをクリックして「検出力分析」セクションを開きます。「有意水準」は0.05に設定されています。
6. 「RMSEの予想値」に0.1と入力します。これは、計画の設定を固定した場合の「濃度」の標準偏差として予想される値です。
そして、「場所」が「濃度」に及ぼす効果に興味があるとします。
係数の予想値
検出力を推定するためには、検出したい差に該当する係数の予想値を設定する必要があります。たとえば、「温度」は、-1と1にコード化された水準を持つ連続因子です。「温度は濃度に影響しない」という帰無仮説の検定に対する検出力について考えてみましょう。Figure 16.14を見ると、「温度」が最小から最大まで変更したときの応答平均の差が0.10である場合、その差を統計的検定で検出できる確率は0.291に過ぎないことが分かります。
1. 「温度」・「時間」・「豆の量」を低水準から高水準に変更したときの、「濃度」における0.10単位の変化を検出できるような検出力を計算するには、各因子の「係数の予想値」を0.05に設定します。低水準から高水準への変化は、コード化した単位で2です。
2. 「挽き」を「Coarse」から「Medium」に変更したときの、「濃度」における0.10単位の変化を検出できるような検出力を計算するには、「挽き」の「係数の予想値」を0.05に設定します。「Coarse」から「Medium」への変化は、コード化した単位で2です。
3. 「場所」を変更したときの、「濃度」における0.10単位の変化を検出できるような検出力を計算するには、「場所 1」と「場所 2」の「係数の予想値」を0.10に設定します。「場所」は、3水準のカテゴリカル因子であるため、「パラメータ」リストでは2つの項(「場所 1」と「場所 2」)で表されます。場所1および場所2が、両方とも、全体平均よりも0.10だけ上回ることは、場所3が全体平均よりも0.20下回ることを意味します。
4. [係数の予想値に基づき変更]をクリックします。「応答の予想値」が指定した係数を反映した値に更新されます。
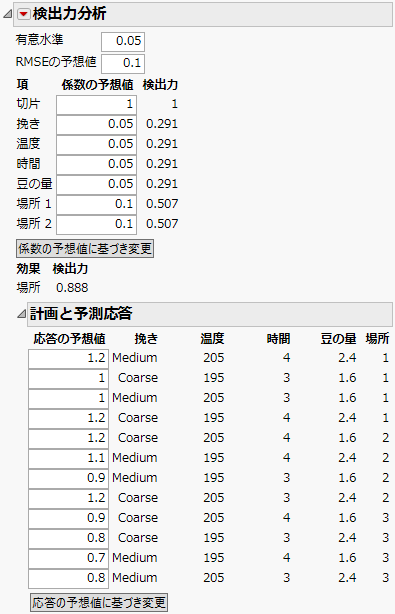
図16.14 入力が完了した「検出力分析」
「検出力分析」表を見ると、最初の4つの因子では、「因子が濃度に影響しない」という帰無仮説の検定に対する検出力が0.291になっています。つまり、各因子が最小から最大まで変化したときの応答平均の差が0.10である場合、その差を統計的検定で検出できる確率は0.291に過ぎません。
「場所」効果全体の検出力は、表の下に表示されているとおり、0.888です。「場所」は3水準のカテゴリカル因子であるため、「検出力分析」の表にある検出力は部分検出力の値です。「場所は濃度に影響しない」という帰無仮説の検定は、F検定です。