媒介分析の例
この例では、「構造方程式モデル」プラットフォームで媒介分析を実行する方法を紹介します。データは、さまざまな背景を持つ生徒が集まった中学校での人種情勢(racial climate)を調べたものです。この例の目的は、「学校への所属感」から「学校への興味」への効果を媒介している「自律性」(autonomy)の役割を調べることです。
1. [ヘルプ]>[サンプルデータフォルダ]を選択し、「Secondary Students.jmp」を開きます。
2. [分析]>[多変量]>[構造方程式モデル]を選択します。
3. [興味]・[所属感]・[自律性]を選択し、[モデルの変数]をクリックします。
4. [OK]をクリックします。
5. [モデルのショートカット]の赤い三角ボタンをクリックし、[横断調査の古典的モデル]>[媒介分析]を選択します。
6. [媒介モデルの指定]ウィンドウで、[原因変数]・[媒介変数]・[結果変数]オプションにそれぞれ「所属感」・「自律性」・「興味」を選択します。
7. [OK]をクリックします。
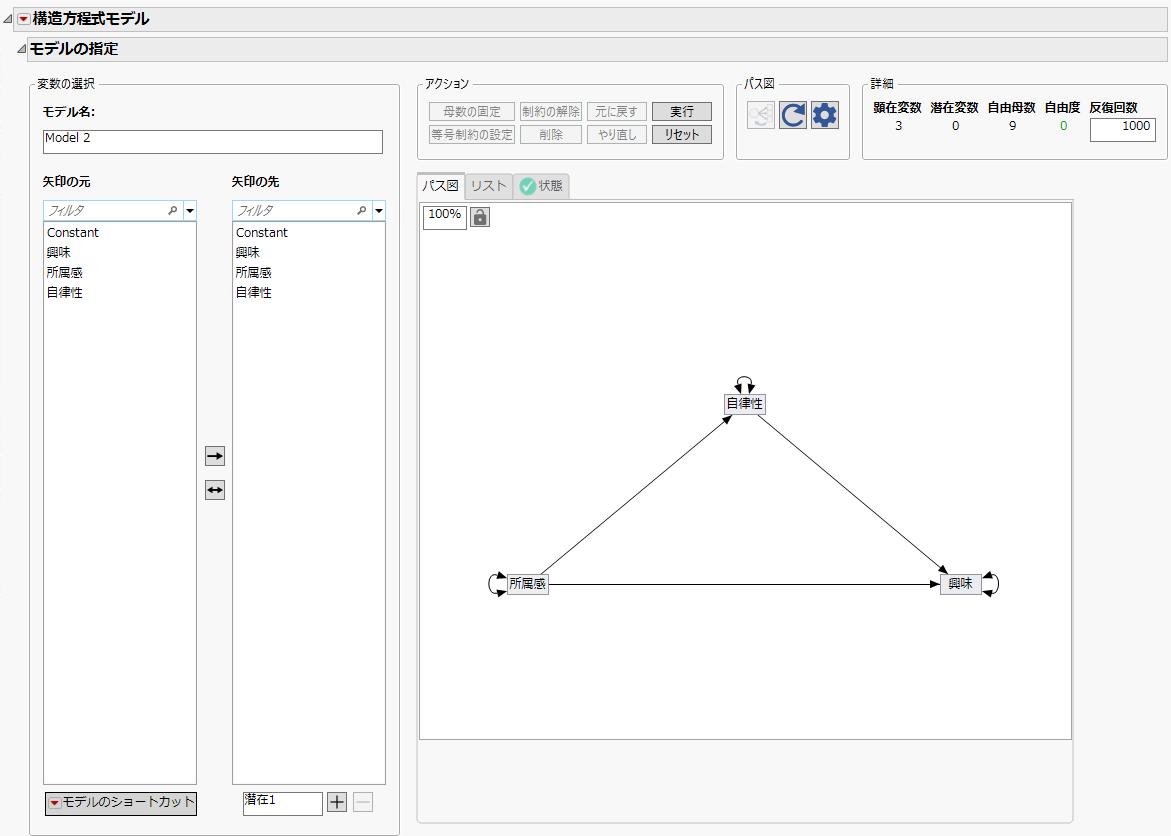
図8.17 構造方程式モデルの指定
8. [実行]をクリックします。
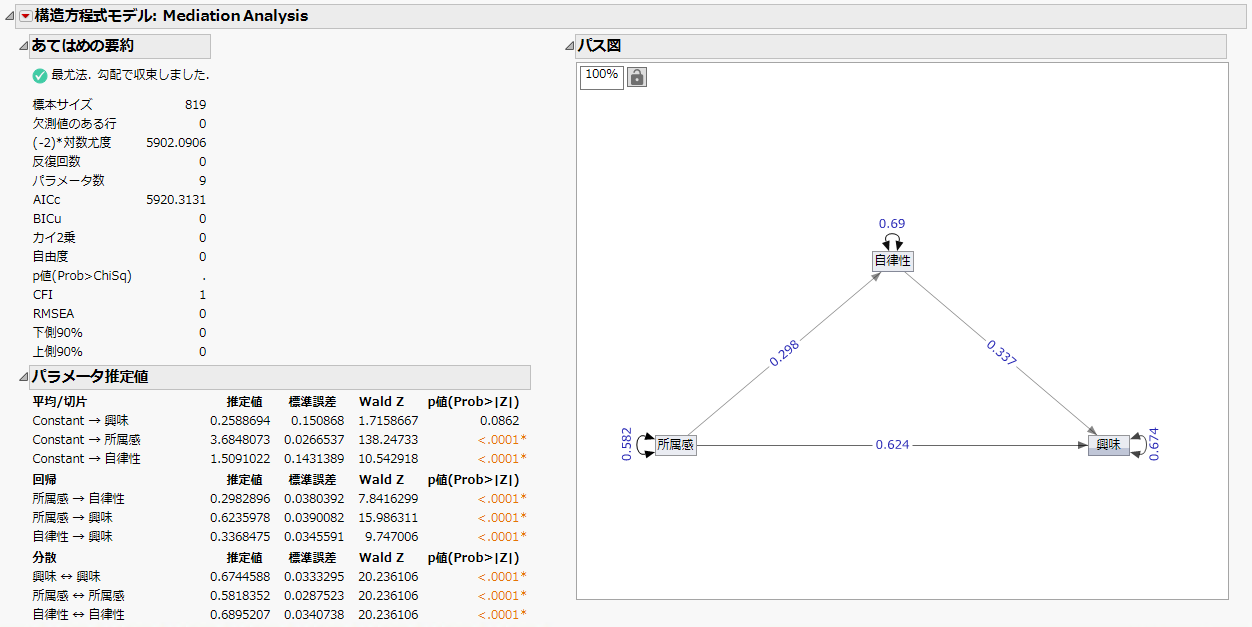
図8.18 「構造方程式モデル」レポート
媒介分析モデルの「あてはめの要約」表と「パラメータ推定値」表が表示されます。「パラメータ推定値」表の回帰係数は、間接効果や総合効果ではなく、直接効果を表しています。「パラメータ推定値」表には、各変数の推定された平均と切片の値、原因変数(「所属感」および「自律性」)と結果変数(「興味」および「自律性」)の間の回帰係数の推定値、および残差分散推定値が含まれています。レポートでは、これらの推定値で表される効果は統計的に有意であることを示しています。これらの推定値に基づいて、次のように結論できるでしょう。
– 「所属感」 ⇒ 「自律性」のパス:「所属感」で1単位異なる二人の学生は、「自律性」で0.298単位異なると推定されます。係数の正符号は、「所属感」が高まるほど、「自律性」も高まる可能性が高いことを示唆しています。
– 「自律性」 ⇒ 「興味」のパス:「所属感」が同じでも、「自律性」で1単位異なる二人の学生は、「興味」で0.337単位異なると推定されます。係数の正符号は、「自律性」の高まるほど、 「興味」も高まる可能性が高いことを示唆しています。
– 「所属感」 ⇒ 「興味」のパス:「所属感」で1単位異なるが、「自律性」が同じである二人の学生は、「興味」で0.624単位異なると推定されます。直接効果は正の値になっています。つまり、「所属感」が高まるほど、「興味」も高まるであろうことを示唆しています。
次に、総合効果と間接効果を計算します。
1. 「構造方程式モデル: 媒介分析」の赤い三角ボタンをクリックし、[総合効果]オプションを選択します。
2. 「構造方程式モデル: 媒介分析」の赤い三角ボタンをクリックし、[間接効果]オプションを選択します。
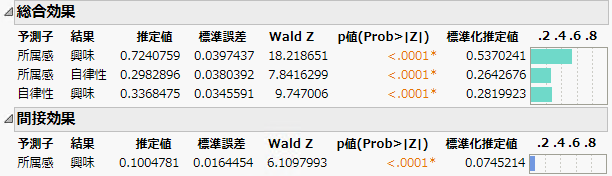
図8.19 全効果と間接効果
「全効果」表には、原因変数(「所属感」および「自律性」)と結果変数(「興味」および「自律性」)の間の総合効果が含まれています。総合効果(total effect)は、結果変数に対する原因変数の直接効果と間接効果を合計したものです。この例では、「所属感」から「自律性」へのパス、および、「自律性」から「興味」までのパスは、直接効果しかありません。そのため、これらの総合効果は、「パラメータ推定値」表の直接効果と同じです。この表は、「所属感」が「興味」に対して、強い正の総合効果(0.724)を持つことを示しています。有意である効果は、「所属感」が「興味」に統計的に有意に寄与していることを示します。総合効果は、媒介変数以外の他の変数を一定に保ちながら、該当の原因変数を1単位だけ変化させた場合の、結果変数の平均変化量を表したものです。たとえば、「所属感」が1単位増加するごとに、「興味」は0.724単位増加すると推定されます。
「間接効果」表には間接効果の推定値が含まれています。これは、「所属感」が「自律性」を経由して「興味」に及ぼす効果です。この表は、「所属感」が媒介変数「自律性」を経由して「興味」に及ぼす間接効果(0.100)が統計的に有意であることを示しています。これは、「所属感」の変化が、媒介変数(「自律性」)の変化を通じて、「興味」に影響を及ぼすことを示唆しています。
結論として、間接効果としては、「所属感」が1単位だけ異なる二人の生徒では、「興味」では0.100単位異なると推定することができます。この間接効果は、「所属感」が高い生徒ほど「自律性」が高く、それが「興味」の増大につながる傾向があることを意味します。
媒介分析における興味の1つは、間接効果を推定することです。しかし、間接効果の推定量の標本分布は、特に標本サイズが小さい場合、非正規分布になる傾向があります。ブートストラップ法を使用すると、この非正規性の問題を解決できます。ブートストラップ法では、間接効果の標本分布を経験分布で近似するために、観測データからの復元抽出を何回も繰り返します。ブートストラップ法は、間接効果について、通常の正規近似よりも、より正確な標準誤差と信頼区間を求めます。
総合効果と間接効果に対するブートストラップ点推定値とブートストラップ信頼区間を得るには、次の手順を行います。
1. ブートストラップ推測を行いたい推定値が含まれている表にて、「推定値」列を右クリックし、[ブートストラップ]を選択します。
2. 「ブートストラップ標本数」に「1000」と入力します。
3. (オプション)Figure 8.20の結果と一致させるには、「乱数シード値」に「1234」と入力します。
4. [OK]をクリックします。
5. 「ブートストラップ結果」テーブルで、「一変量の分布」スクリプトを実行します。
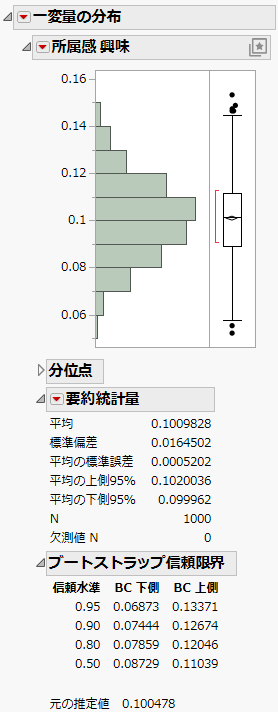
図8.20 ブートストラップのレポート
表示されるレポートには、ブートストラップ推定値の分布に関する情報が含まれています。「統計の要約」表は、間接効果のブートストラップ推定値が0.101であることを示しています。この推定値は、Figure 8.19で示した間接効果の推定値とほぼ同じです。 「ブートストラップ信頼限界」レポートには、推定された間接効果のバイアス補正された信頼限界が含まれています。95%信頼区間にはゼロが含まれません。これは媒介分析における間接効果の有意性を示しています。
ヒント: なお、「構造方程式モデル」の赤い三角ボタンの[推測方法]>[ブートストラップ推測]を使用すれば、モデルに含まれるすべてのパラメータ推定値や効果に関して、ブートストラップ推測を行えます。