ノンパラメトリックな検定のレポート
「一元配置」プラットフォームには、平均を比較するためのノンパラメトリックなオプションが用意されています。ここでは、ノンパラメトリックなオプションのレポートを取り上げます。
ノンパラメトリックな検定では、（分布の形状が同じであるという仮定が正しければ）「グループ間で平均または中央値が等しい」などの帰無仮説に対する検定が行われます。ノンパラメトリックな検定では、「順位スコア」と呼ばれる、Y変数の順位から変換された値が使用されます。Hajek（1969）およびSAS Institute Inc.（2023a）を参照してください。ノンパラメトリックな多重比較では、ペアの比較を繰り返すことによる全体的な誤りの確率も調整されます。ノンパラメトリックな多重比較のレポートを参照してください。
Wilcoxon / Kruskal-Wallis検定、メディアン検定、Friedman順位検定、Van der Waerden検定のレポート
「一元配置」プラットフォームの［Wilcoxon / Kruskal-Wallis検定］・［メディアン検定］・［Friedman順位検定］・［Van der Waerden検定］では、要約統計量と検定結果を示す表が2～3つ作成されます。要約統計量の表には以下の列があります。
水準
Xの水準。
度数
各群の標本サイズ（各水準の度数）。
スコア和
各水準の順位スコアの和。
スコアの期待値
水準間に差はないという帰無仮説のもとでのスコアの期待値。
スコア平均
各水準の平均順位スコア。
(平均-平均0)/標準偏差0
標準化したスコア。「平均0」は帰無仮説のもとでの平均スコアの期待値で、「標準偏差0」は帰無仮説のもとでの平均スコアの標準偏差です。帰無仮説は、「（すべての群で分布の形状が同じという仮定が正しいもとで）どの群の平均やメディアンもまったく同じである」というものです。
「2標本検定 (正規近似)」表
X変数の水準数が2の場合、「2標本検定 (正規近似)」表には次の列が含まれます。
S
標本サイズが小さいほうの水準の順位スコアの和。
Z
正規近似の検定統計量。ここでの結果は、0.5の連続修正を行っています。2標本の場合における正規近似を参照してください。
p値(Prob>Z)
正規近似の片側検定のp値。ここでの結果は、0.5の連続修正を行っています。p値は、0.5連続修正を行った検定統計量に基づき、標準正規分布により求められます。
p値(Prob>|Z|)
正規近似のp値。ここでの結果は、0.5の連続修正を行っています。p値は、0.5連続修正を行った検定統計量に基づき、標準正規分布により求められます。
メモ: Wilcoxon/Kruskal-Wallisの検定（順位和）レポートでは、この表は「Wilcoxon 2標本検定 (正規近似)」表という名前です。
「一元配置検定 (カイ2乗近似)」表
「一元配置（またはKruskal-Wallis）検定 (カイ2乗近似)」表は、カイ2乗近似による検定結果を示しています。Conover（1999）を参照してください。グループ数が2群の場合、Kruskal-Wallis検定はWilcoxon検定と等価です。ただし、グループ数が2群の場合、JMPの「Wilcoxon検定」では0.5連続修正を行っており、「Kruskal-Walls検定」では0.5連続修正を行っていません。
カイ2乗
カイ2乗検定統計量の値。一元配置のカイ2乗近似を参照してください。
自由度
検定の自由度。
p値(Prob>ChiSq)
検定のp値。このp値はXの水準数から1を引いた値を自由度にしたカイ2乗分布に基づいています。グループ数が2群の場合、このp値は、Wilcoxon検定のp値です。ただし、ここでの結果は、0.5連続修正を行わないWilcoxon検定の結果となっています。
メモ: Wilcoxon/Kruskal-Wallisの検定（順位和）レポートでは、この表は「Kruskal-Wallis検定 (カイ2乗近似)」表という名前です。
Friedman-Nemenyi検定
「Friedman順位検定」の赤い三角ボタンのメニューには、Nemenyi検定のオプションが含まれています。この検定は、Tukey-Kramerの多重比較検定のノンパラメトリック版です。Friedman順位検定が統計的に有意である場合は、Nemenyi検定を使ってどのペアが異なるかを評価します。要約表には以下の列があります。
水準
比較対象のペアのうち、1つ目の水準。
- 水準
比較対象のペアのうち、2つ目の水準。
スコア平均の差
1つ目の水準（「水準」）の順位スコアの平均から、2つ目の水準（「-水準」）の順位スコアの平均を引いた値。
Z
検定統計量。この検定統計量は、「（「すべての群の分布の形状が同じ」という仮定が正しい場合において）分布の位置に差がない」という帰無仮説のもとで、漸近的に標準正規分布に従います。
p値
Zに基づく漸近検定のp値。
レポートに、検定の要約統計量を表示した2つのアウトラインが追加されます。
ペアごとのp値
ペアごとのp値の行列。要約表にある値と同じです。
文字の接続レポート
文字によって有意差があるかどうかを示したレポート。文字で繋がっていない平均のペアには有意差があります。
Kolmogorov-Smirnov二標本検定のレポート
「一元配置」プラットフォームの［Kolmogrov Smirnov二標本検定］レポートでは、要約表と「漸近Kolmogrov-Smirnov検定」表の2つが作成されます。要約表には以下の列があります。
水準
X変数の2つの水準。
度数
各水準の度数。
最大時の経験分布関数
2つの経験累積分布関数（EDF）の差が最大になるときの、各水準のEDFの値。「合計」という行には、2つのEDFの差が最大になるときの、プーリングしたEDF（データセット全体のEDF）の値が示されます。
最大時の平均からの乖離
各水準について、以下の手順に従って求めた値です。
– 該当の水準における経験分布関数と、データセット全体（合計）のプーリングした経験分布関数との差を、群間差が最大となっている個所で求める。
– この差に、その水準における観測値の度数の平方根を掛ける。
「漸近Kolmogrov-Smirnov検定」表には次の列があります。
KS
Kolmogorov-Smirnov統計量は次式で計算されます。
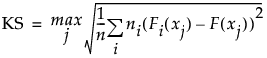
この式では、次のような表記を使用しています。
– xj (j = 1, ..., n)は、標本サイズ
– niは、Xのi番目の水準の標本サイズ
– Fは、プーリングした経験累積分布関数
– Fiは、Xのi番目の水準の経験累積分布関数
メモ: このKolmogorov-Smirnov統計量はX変数に3つ以上の水準がある場合でも当てはまりますが、JMPでは、X変数の水準数が2である場合にのみKolmogorov-Smirnov検定が使えます。
Ksa
漸近的なKolmogorov-Smirnov統計量。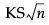
で求められます。ここで、nは、全体の標本サイズ（観測値数）です。
D=max|F1-F2|
2群のEDFの差で、その絶対値が最大のもの。2つの標本を比較するために使用されるKolmogorov-Smirnov統計量です。
p値(Prob > D)
両側検定のp値。「2群の分布はまったく同じである」という帰無仮説のもとで、Dが求められた値よりも大きくなる確率です。
D+ = max(F1-F2)
有意であれば、「1つ目の水準が2つ目の水準を上回る」という対立仮説が採択される片側検定の検定統計量。
p値(Prob > D+)
D+に基づく検定のp値。
D- = max(F2-F1)
有意であれば、「2つ目の水準が1つ目の水準を上回る」という対立仮説が採択される片側検定の検定統計量。
p値(Prob > D-)
D-に基づく検定のp値。
正確検定のレポート
「一元配置」プラットフォームでは、X変数が2水準の場合に、各種ノンパラメトリック検定の正確検定を実行することができます。Wilcoxon / Kruskal-Wallis検定、メディアン検定、およびVan der Waerden検定では、次の列を含む「二標本: 正確検定」表が作成されます。
S
標本サイズが小さいほうの水準の順位スコアの和。両水準における観測値の個数が等しい場合は、値の順序で並べて後になる水準を使用します。
p値(Prob £ S)
片側検定のp値。この検定の方向は、X変数の2つの水準間にある差の符号によって決まります。
p値(Prob ≥ |S-Mean|)
両側検定のp値。
メモ: 正確Kolmogorov-Smirnov検定の表には、漸近検定と同じ統計量が表示されます。ただし、p値は正確な確率です。Kolmogorov-Smirnov二標本検定のレポートを参照してください。