直接的なモデル推定の統計詳細
「関数データエクスプローラ」で利用できる直接的なモデル推定は、行列分解に基づいています。まず、データが、行列の各行が各関数、各列が入力変数の各値になっている行列に変換されます。この積み重ねた行列の各行はID変数の1つの水準に対する全出力関数に対応し、各列は入力変数の水準に対応します。直接的なモデル推定では、この積み重ねた行列に対して何らかの行列分解を実行することによって、関数主成分分析を行います。いくつかの直接法で使用される行列分解の1つは特異値分解（SVD; singular value decomposition）です。
nxpの行列Xの特異値分解は、次のように表すことができます。
X ≈ UDV′
行列U、D、Vは次の性質を持ちます。
• Uはn × rはスコアを表す直交行列であり、U′U = Irとなっています。
• Vはp × rの因子負荷量を表す直交行列であり、V′V = Irとなっています。
• Dはr × rの対角行列であり、正の特異値skを対角要素に持ちます。
• r << min(n, p)
Vの列は形状関数に対応し、特異値は固有値に対応します。データ内の各関数は、形状関数（Vの列）の線形結合を用いて近似できます。
罰則付き特異値分解
罰則付き特異値分解法は、積み重ね行列を一度に1次元ずつ分解します。これは、特異値分解でXで最良のランク1近似を1次元ずつ見つけていくことを意味します。Xのランク1近似で近似値を見つけることは、次のように記述されるFrobeniusノルムを最小化するのと同じことです。
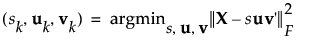
ペナルティパラメータ（罰則パラメータ）を追加した場合の最小化関数は次のように定義されます。
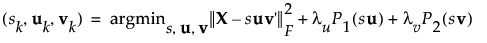
ここで、P1(su)とP2(sv)は、結果をスパース（希薄）にするためのペナルティ（罰則）です。
各次元kに対して、次の処理が実行されます。
1. 標準的な特異値分解を実行して、初期値を取得します。
2. uを固定し、lassoペナルティを用いた罰則付き回帰を実行して、vを求めます。このとき、検証にはAICcを使用します。
3. vを固定し、lassoペナルティを用いた罰則付き回帰を実行して、uを求めます。このとき、検証にはAICcを使用します。
4. uとvが収束するまで、step 2とstep 3を繰り返します。
詳細については、Lee et al（2010）を参照してください。
非負値特異値分解
非負値特異値分法は、以下の追加の制約を課した状態で、積み重ねた行列に対して特異値分解を実行します。
X ≈ UDV′ ここでUij ≥ 0およびVij ≥ 0
この手法では、制約付き最小2乗法を用いてUとVを求めます。
多変量スペクトル分離
多変量スペクトル分離（MCR; multivariate curve resolution）も行列分解を使用しますが、データの積み重なった行列を3つではなく、2つの行列に分解します。n × pの行列Xの行列分解は、次のように表すことができます。
X ≈ CS′
行列CとSには以下の性質があります。
Cij ≥ 0
Sij ≥ 0
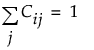（つまり、Cの各行の合計が1になるように制約されています。）
Sの列は、非負の形状関数です。 Cの行は、配合物の配合割合を表します。これにより、各個別の関数について、割合を表すスコアの和が1で、その割合で形状関数を混合したものによって、Xを近似します。