정준 그림 및 정준 구조
"판별 분석" 보고서의 "정준 그림"은 변수의 정준 상관 구조를 설명하는 행렬도입니다.
정준 구조
"X, 범주" 열의 각 수준은 표시 변수를 정의합니다. 범주를 나타내는 표시 변수 집합과 공변량 간에 정준 상관이 수행됩니다. 여기서 공변량의 선형 결합, 즉 정준 변수가 도출됩니다. 이러한 정준 변수는 범주 간 변동을 요약하려고 합니다.
첫 번째 정준 변수는 범주 표시 변수와 공변량 간의 다중상관을 최대화하는 공변량 선형 결합입니다. 두 번째 정준 변수는 첫 번째 정준 변수와 상관관계가 없으며 범주와의 다중상관을 최대화하는 선형 결합입니다. "X, 범주" 열에 k개의 수준이 있으면 정준 변수의 수가 k - 1개입니다.
정준 그림
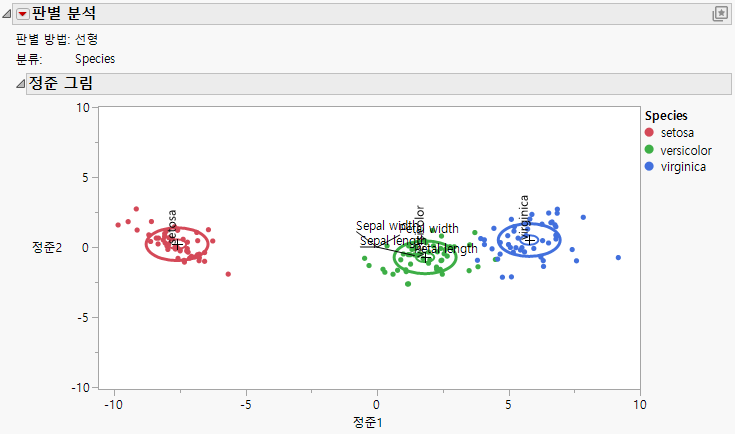
Figure 5.7에서는 Iris.jmp 데이터 테이블의 선형 판별 분석에 대한 정준 그림을 보여 줍니다. Species별로 점에 색상이 적용되어 있습니다.
그림 5.7 Iris.jmp에 대한 정준 그림
행렬도 축은 처음 두 정준 변수입니다. 이는 그룹 간에 최대 분리를 제공하는 두 차원을 정의합니다. 각 정준 변수는 공변량의 선형 결합입니다. 자세한 내용은 정준 구조에서 확인하십시오. 행렬도에서는 각 관측값이 정준 변수에 따라 어떻게 표시되는지 그리고 각 공변량이 정준 변수에 어떻게 기여하는지 보여 줍니다.
• 각 그룹의 관측값 및 다변량 평균은 행렬도에 점으로 표시됩니다. 이는 처음 두 정준 변수로 표현됩니다.
– 각 다변량 평균에 해당하는 점은 더하기("+") 표식으로 나타냅니다.
– 각 평균에 대해 95% 신뢰 수준 타원이 그림에 표시됩니다. 두 그룹이 유의하게 다르면 신뢰도 타원이 교차하지 않는 경향이 있습니다.
– 각 그룹에 대해 50% 등고선을 나타내는 타원이 그림에 표시됩니다. 이는 정규성을 가정하고 처음 두 정준 변수의 공간에서 관측값의 약 50%를 포함하는 영역을 나타냅니다.
• 그림에 표시되는 선 집합은 공변량을 나타냅니다.
– 각 정준 변수에 대해 선형 결합된 공변량의 계수를 가중치로 해석할 수 있습니다.
– 가중치 간에 쉽게 비교하기 위해 각 공변량이 평균이 0, 표준편차가 1이 되도록 표준화됩니다. 표준화된 공변량의 계수를 정준 가중치라고 합니다. 공변량의 정준 가중치가 클수록 정준 변수와의 연관성이 커집니다.
– 행렬도에서 각 선의 길이와 방향은 해당 공변량과 처음 두 정준 변수의 연관성 정도를 나타냅니다. 선 길이는 정준 가중치의 배수입니다.
– 선은 데이터의 총 평균을 정준 변수 측면에서 나타내는 점 (0,0)에서 시작됩니다.
– "판별 분석"의 빨간색 삼각형 메뉴에서 정준 옵션 > 정준 상세 정보 표시를 선택하여 가중치 계수 값을 얻을 수 있습니다. "정준 상세 정보" 보고서 맨 아래에서 "표준화 스코어링 계수"를 클릭합니다. 자세한 내용은 표준화 스코어링 계수에서 확인하십시오.
정준 그림 수정
다음과 같이 추가 옵션을 사용하여 행렬도를 수정할 수 있습니다.
• "판별 분석"의 빨간색 삼각형 메뉴에서 정준 옵션 > 평균 CL 타원 표시를 선택하여 95% 신뢰도 타원을 표시하거나 숨깁니다.
• "판별 분석"의 빨간색 삼각형 메뉴에서 정준 옵션 > 행렬도 선 표시를 선택하여 선을 표시하거나 숨깁니다.
• 행렬도 선의 가운데를 그래프의 다른 위치로 드래그합니다. "판별 분석"의 빨간색 삼각형 메뉴에서 정준 옵션 > 행렬도 선 위치를 선택하여 위치와 척도를 지정합니다. 선을 표시하기 위해 조정이 필요한 경우를 제외하고 정준 그림의 기본 반지름 척도는 1.5입니다.
• "판별 분석"의 빨간색 삼각형 메뉴에서 정준 옵션 > 정규 50% 등고선 표시를 선택하여 50% 등고선을 표시하거나 숨깁니다.
• "판별 분석"의 빨간색 삼각형 메뉴에서 정준 옵션 > 점에 색 적용을 선택하여 타원과 일치하도록 점에 색상 코딩을 적용합니다.
세 개 이상의 범주로 분류
Iris.jmp 데이터의 경우 세 개의 Species가 있으므로 정준 변수는 두 개뿐입니다. Figure 5.7의 그림에서는 두 정준 변수를 사용하여 세 그룹을 양호하게 분리한 상태를 보여 줍니다.
그림의 선은 다음을 나타냅니다.
• Petal length는 정준1과 양의 관계를 갖고 정준2와 음의 관계를 갖습니다. 따라서 정준2보다 정준1을 정의하는 데 가중치를 더 부여합니다.
• Petal width는 정준1 및 정준2와 모두 양의 관계를 갖습니다. 따라서 두 정준 변량을 정의하는 데 동일한 가중치를 부여합니다.
• Sepal width는 정준1과 음의 관계를 갖고 정준2와 양의 관계를 갖습니다. 따라서 정준1보다 정준2를 정의하는 데 가중치를 더 부여합니다.
• Sepal length는 정준1을 정의할 때 음의 가중치를 가지며 정준2를 정의할 때 매우 약하게 연관됩니다.
두 개의 범주로 분류
분류 변수의 수준이 두 개뿐인 경우 그림에서 "정준1"로 표시되는 단일 정규 변수에 대해 점이 표시됩니다. 각 공변량의 정준 가중치는 정준1에만 관련됩니다. 선은 공변량을 분리하기 위해 연직 성분으로만 표시됩니다. 선을 정준1 축에 투영하여 단일 정준 변수와의 상대적 연관성을 비교할 수 있습니다.
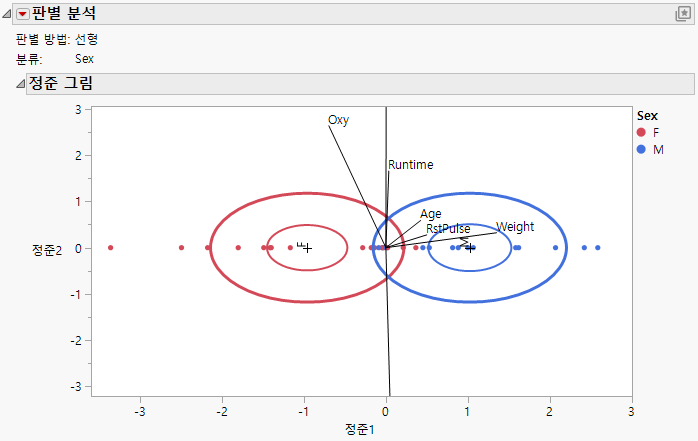
Figure 5.8에서는 Fitness.jmp 샘플 데이터 테이블에 대한 정준 그림을 보여 줍니다. 7개의 연속형 변량이 개인을 범주 M(남성) 또는 F(여성)로 분류하는 데 사용됩니다. 분류 변수의 범주가 두 개뿐이므로 정준 변수가 하나만 있습니다.
그림 5.8 Fitness.jmp에 대한 정준 그림
정준 그림의 점에 Sex별로 색상이 적용되어 있습니다. 두 그룹은 정준1의 값으로 잘 분리되어 있습니다.
7개의 공변량에 해당하는 선에 연직 성분이 있지만 이 경우 선을 정준1 축에 대한 투영의 관점으로만 해석해야 합니다. 다음 사항에 유의하십시오.
• MaxPulse, Runtime 및 RunPulse는 정준1과 연관성이 거의 없습니다.
• Weight, RstPulse 및 Age는 정준1과 양의 관계를 갖습니다. Weight의 연관성이 가장 높습니다. RstPulse 및 Age 공변량은 연관성이 비슷하지만 더 작습니다.
• Oxy는 정준1과 음의 관계를 갖습니다.