기울기가 동일한 공분산 분석의 예
모형 적합 플랫폼의 표준 최소 제곱 분석법을 사용하여 공분산 분석 모형을 적합시킵니다. 공분산 분석 모형은 기본 관심 요인과 공변량 항이 있는 모형입니다. 공변량은 기본 관심 요인은 아니지만 기본 요인이 반응에 미치는 효과에 영향을 줄 수 있는 요인입니다. 이 예에서는 drug가 기본 관심 요인이고 x가 공변량입니다.
참고: 이 분석에서는 공변량이 기본 요인의 각 수준에 유사한 방식으로 영향을 미친다고 가정합니다. 즉, 기울기가 동일한 공분산 모형입니다. 모형에 교호작용 항이 포함되지 않습니다. 기울기가 다른 모형에 대한 내용은 기울기가 다른 공분산 분석의 예에서 확인하십시오.
1. 도움말 > 샘플 데이터 폴더를 선택하고 Drug.jmp를 엽니다.
2. 분석 > 모형 적합을 선택합니다.
3. y를 선택하고 Y를 클릭합니다.
4. Drug와 x를 모두 선택하고 추가를 클릭합니다.
5. 실행을 클릭합니다.
아래에 보고서 섹션이 표시되고 설명이 나옵니다.
회귀 그림 및 실제값 대 예측값 그림
회귀 그림 및 실제값 대 예측값 그림을 사용하여 모형을 평가하고 공변량이 반응에 미치는 영향을 파악할 수 있습니다.
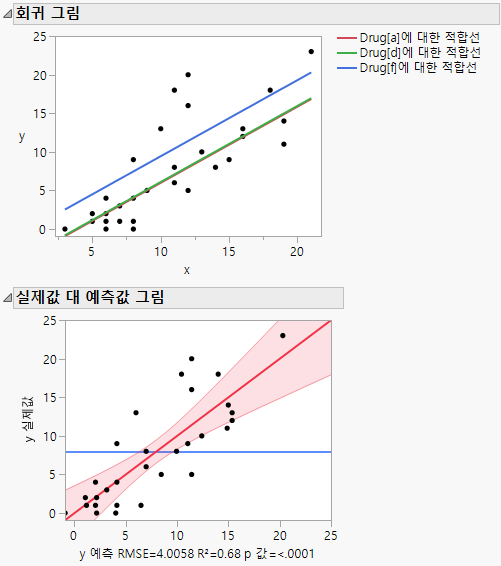
그림 4.20 기울기가 동일한 공분산 분석의 그림
"회귀 그림"에서는 기울기가 동일한 모형이 적합되었음을 보여 줍니다. 반응은 각 약물에 대해 동일한 비율로 공변량 x에 따라 증가합니다. 공변량 x의 수준 전체에서 Drug f에 대한 반응이 가장 높습니다.
적합 결여
약물 데이터 테이블에는 반복된 관측값이 포함되어 있습니다. 예를 들어 행 1과 9는 둘 다 Drug = a이고 x = 11입니다. 모형을 적합시킬 때 반복된 관측값을 사용하여 변동의 순수 오차 추정값을 생성할 수 있습니다. 공변량의 지정되지 않은 함수 형식 또는 명목형 효과의 교호작용에 대한 또 다른 오차 추정값을 생성할 수 있습니다. 이러한 추정값은 적합 결여 검정의 기반이 됩니다. 적합 결여 오차가 유의하면 데이터의 일부 효과가 모형에 의해 설명되지 않음을 나타냅니다. 자세한 내용은 적합 결여에서 확인하십시오.
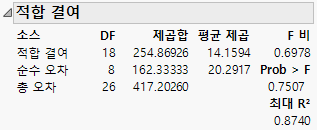
그림 4.21 기울기가 동일한 공분산 분석의 적합 결여 검정
"적합 결여" 보고서의 "Prob > F" 값 0.7507에서 알 수 있듯이 적합 결여 오차는 유의하지 않습니다.
최소 제곱 평균
최소 제곱 평균으로 공변량을 고려하여 각 약물 수준에 대한 평균 반응을 비교합니다.
최소 제곱 평균은 공변량이 반응에 미치는 효과에 대해 수정되므로 일반 평균과 다릅니다. 최소 제곱 평균은 공변량 x가 평균 값 10.7333으로 고정될 때 Drug의 세 가지 각 수준에 대해 예측된 값입니다.
최소 제곱 평균은 "모수 추정값" 보고서에 제공된 모수 추정값을 사용하여 계산됩니다.
예측 표현식
-2.696 - 1.185*Drug[a] - 1.0761*Drug[d] + 0.98718*x
a:
-2.696 - 1.185*(1) -1.0761*(0) + 0.98718*(10.7333) = 6.71
d:
-2.696 - 1.185*(0) -1.0761*(1) + 0.98718*(10.7333) = 6.82
f:
-2.696 - 1.185*(-1) -1.0761*(-1) + 0.98718*(10.7333) = 10.16
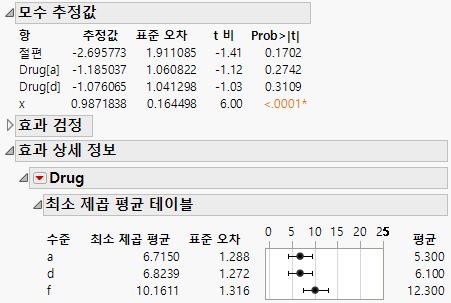
그림 4.22 Drug 테스트 데이터에 대한 모수 추정값 및 최소 제곱 평균