예: 혼합 모형 분석법 사용

이 예에서는 모형 적합 플랫폼의 혼합 모형 분석법을 사용하여 절편과 기울기 간의 상관관계를 위한 모형을 적합시키는 방법을 보여 줍니다. 밀 수확량 연구에서 건조 기후 조건에 맞게 적응된 경질 붉은 겨울밀 품종 모집단에서 10종의 밀을 무작위로 선택합니다. 그런 다음 6개의 1에이커 대지에 무작위로 할당합니다. 예정지의 수분 함량은 발아율에 영향을 줄 수 있으며 결과적으로 최종 수확량이 달라질 수 있습니다. 따라서 각 대지에 대해 상위 36인치 토양의 예정지 수분 양이 결정됩니다. 이 연구에서 수분 함량이 수확량에 영향을 주는지 여부를 확인하는 데 관심이 있습니다.

품종이 무작위로 선택되므로 각 품종에 대한 회귀 모형은 품종 모형 모집단에서 선택한 랜덤 모형입니다. 절편과 기울기는 각 품종에 대해 랜덤하며 상관관계가 있을 수 있습니다. 랜덤 계수는 고정 효과에서 중심화됩니다. 고정 효과는 모집단 절편과 기울기이며, 이는 품종의 절편과 기울기 모집단에 대한 기대값입니다. 이 예는 Littell et al. 연구 자료 (2006, p. 320)에서 가져왔습니다.

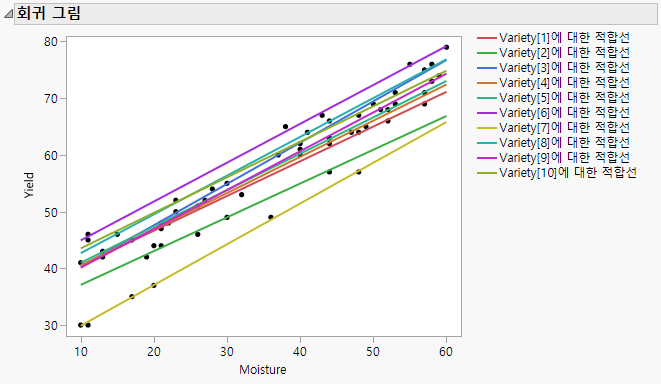
표준 최소 제곱 분석법에서 REML을 사용하여 모형을 적합시키면 절편과 기울기의 변동을 볼 수 있습니다(Figure 8.2). 기울기의 변동성은 크지 않지만 절편은 상당한 차이가 있습니다. 절편과 기울기는 음의 상관관계가 있을 수 있으며 절편이 낮은 품종의 기울기가 더 높은 것으로 보입니다.

그림 8.2 표준 최소 제곱 회귀 

절편과 기울기 간의 상관관계를 모델링하기 위해 혼합 모형 분석법을 사용합니다. 이를 통해 모집단 회귀 방정식과 품종별 방정식을 결정하려고 합니다.

1. 도움말 > 샘플 데이터 폴더를 선택하고 Wheat.jmp를 엽니다.

2. 분석 > 모형 적합을 선택합니다.

3. Yield를 선택하고 Y를 클릭합니다.

이 열을 Y로 추가하면 적합 분석법이 "표준 최소 제곱"으로 설정됩니다.

4. "분석법" 목록에서 혼합 모형을 선택합니다. 아니면 "혼합 모형" 분석법을 먼저 선택한 후 Y를 클릭하여 Yield를 추가할 수도 있습니다.

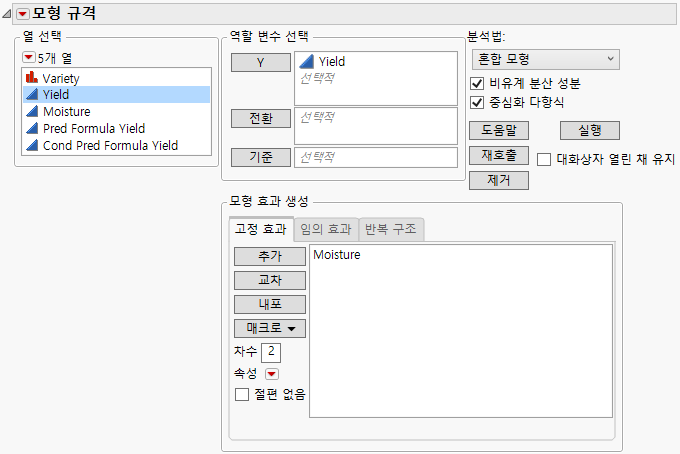
5. Moisture를 선택하고 "고정 효과" 탭에서 추가를 클릭합니다.

그림 8.3 고정 효과를 보여 주는 완료된 모형 적합 시작 창 

6. 임의 효과 탭을 선택합니다.

7. Moisture를 선택하고 추가를 클릭합니다.

8. "열 선택" 목록에서 Variety를 선택하고 "임의 효과" 탭에서 Moisture를 선택한 후 내포 랜덤 계수를 클릭합니다.

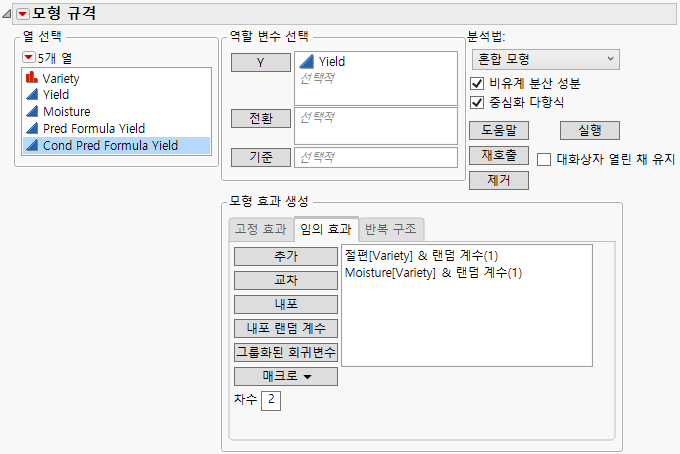
그림 8.4 임의 효과 탭을 보여 주는 완료된 모형 적합 시작 창 

임의 효과는 품종별로 그룹화되고 절편은 랜덤 성분으로 포함됩니다.

9. (선택 사항) "모형 규격"의 빨간색 삼각형을 클릭하고 중심화 다항식 옵션의 설정을 확인합니다.

Moisture 효과는 임의 효과로 포함되어 있으므로 "중심화 다항식" 옵션이 선택되어 있더라도 평균으로 중심화되지 않습니다.

10. 실행을 클릭합니다.

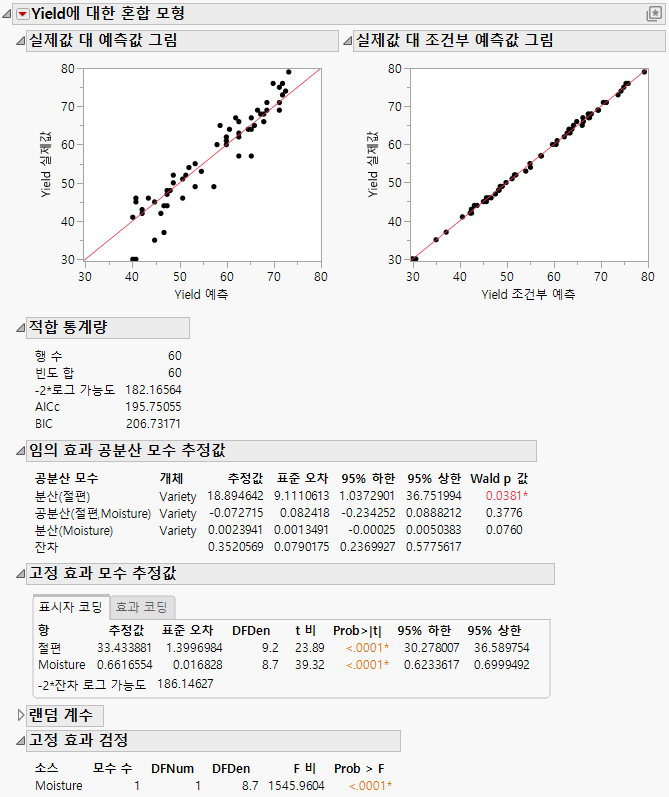
Figure 8.5에 "혼합 모형" 보고서가 표시되어 있습니다. "실제값 대 예측값 그림"은 모형 적합 및 기본 가정에 대해 불일치를 나타내지 않습니다.

모형 적합에 명백한 문제가 없으므로 통계 검정을 해석하고 회귀 방정식을 구할 수 있습니다. "고정 효과 검정" 보고서에서 볼 수 있듯이 수확량에 대한 수분의 효과는 유의합니다. "고정 효과 모수 추정값"에 제공된 추정값은 다음 방정식이 추정된 모집단 회귀 방정식임을 나타냅니다.

Yield = 33.43 + 0.66 * Moisture

"임의 효과 공분산 모수 추정값" 보고서에는 품종의 절편 분산을 나타내는 "분산(절편)", 기울기를 나타내는 "분산(Moisture)" 및 공분산을 나타내는 "공분산(절편, Moisture)"의 추정값이 제공됩니다. 이 경우 절편과 기울기는 추정값의 신뢰 구간에 0이 포함되므로 유의한 상관관계가 없습니다. 이 보고서에는 잔차 분산의 추정값도 제공됩니다.

그림 8.5 혼합 모형 보고서 

모집단 회귀 방정식의 추정값이 있지만 품종(Variety) 2의 추정 수확량에도 관심이 있습니다.

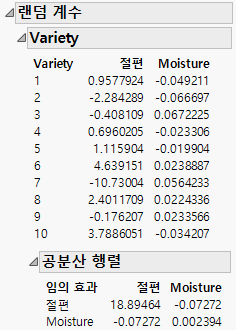
11. "랜덤 계수" 보고서를 열어 "절편" 및 "Moisture"에 대한 품종 효과의 추정값을 확인합니다. 이러한 계수는 각 품종이 모집단과 어떻게 다른지 추정합니다.

그림 8.6 랜덤 계수 보고서 

"고정 효과 모수 추정값" 및 "랜덤 계수" 보고서에서 Variety 2에 대해 다음과 같은 예측 방정식을 구합니다.

Yield = 33.433 + 0.662 * Moisture – 2.284 – 0.067 * Moisture

Yield = 31.149 + 0.595 * Moisture

Variety 2는 모집단 평균보다 낮은 수확량으로 시작하여 모집단 평균보다 낮은 비율로 Moisture와 함께 증가합니다.