모형 보고서
시계열 플랫폼에서 "ARIMA", "계절 ARIMA" 및 "평활 모형" 옵션은 비슷한 모형 보고서를 생성합니다. 이러한 모델링 옵션은 이론적 모형을 계열에 적합시키고 적합 모형을 사용하여 계열의 미래 값을 예측하는 데 사용됩니다. 또한 이러한 옵션을 사용하면 선택한 모형의 적합성을 확인할 수 있는 통계량 및 잔차가 생성됩니다. 모델링 옵션을 여러 번 선택할 수 있습니다. 모형을 선택할 때마다 해당 모형이 모형 비교 테이블에 추가됩니다. 모형 비교 테이블에서 모형 옆의 "보고서" 체크박스를 선택하면 해당 모형에 대한 보고서가 생성됩니다. 보고서 제목에 모형이 지정됩니다.
기본적으로 다음 보고서가 표시됩니다.
• 모형 요약 테이블
• 모수 추정값 테이블
• 예측 그림
• 잔차
• 반복 기록
모형 요약 테이블
모형에 대한 적합 통계량을 포함합니다. 아래 계산식에서 n은 계열의 길이이고 k는 모형에 있는 적합 모수의 수입니다.
DF
적합의 자유도입니다(n – k).
개변 제곱합
개변 제곱의 합입니다.
잔차 제곱합
잔차 제곱의 합입니다.
분산 추정값
개변 제곱합을 자유도(n – k)로 나눈 값입니다. 이 값은 ARIMA 모형 섹션에 설명된 확률 충격 at의 분산에 대한 표본 추정값입니다.
표준편차
분산 추정값의 제곱근입니다. 이 값은 확률 충격 at의 표준편차에 대한 표본 추정값입니다.
Akaike 정보 기준
-2*로그 가능도 + 2k로 계산되는 AIC 값입니다. AIC 값이 작을수록 더 나은 적합을 나타냅니다.
Schwarz 베이지안 기준
-2*로그 가능도 + k*ln(n)으로 계산되는 SBC 값입니다. SBC 값이 작을수록 더 나은 적합을 나타냅니다. Schwarz 베이지안 기준은 BIC(베이지안 정보 기준)와 같습니다.
R²
다음과 같이 계산되는 R² 값입니다.
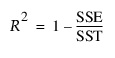
다음은 각 요소에 대한 설명입니다.
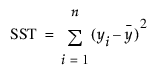
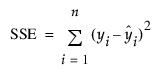
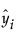1시차 후 예측
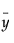평균
모형이 계열에 잘 적합되지 않으면 모형 SSE(오차 제곱합)가 SST(총 제곱합)보다 클 수 있습니다. 따라서 R2이 음수일 수 있습니다.
Adj-R²
다음과 같이 계산되는 수정 R2 값입니다.
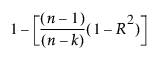
MAPE
다음과 같이 계산되는 평균 절대 백분율 오차 값입니다.
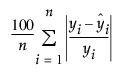
MAE
다음과 같이 계산되는 평균 절대 오차 값입니다.
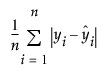
-2*로그 가능도
최량 적합 모수 추정값에서 계산된 음의 로그 가능도 함수의 두 배입니다. 값이 작을수록 더 나은 적합을 나타냅니다. 자세한 내용은 가능도, AICc 및 BIC의 선형 모형 적합에서 확인하십시오.
안정적
자기회귀 연산자가 안정적인지 여부를 나타냅니다. 즉, f(z) = 0의 모든 제곱근이 단위 원을 벗어나는지 여부입니다.
가역적
이동 평균 연산자가 가역적인지 여부를 나타냅니다. 즉, q(z) = 0의 모든 제곱근이 단위 원을 벗어나는지 여부입니다.
참고: F 및 q 연산자는 ARIMA 모형 섹션에 정의되어 있습니다.
모수 추정값 테이블
시계열 모형 모수의 추정값을 표시합니다. 각 모형 유형마다 고유한 모수 집합이 있으며, 이러한 모수는 특정 시계열 모형에 대한 섹션에 설명되어 있습니다. 각 모수 추정값 테이블에는 다음과 같은 열이 포함됩니다.
항
각 모형 유형에 대한 섹션에 설명된 모수의 이름입니다. 일부 모형에는 절편 또는 평균 항이 포함됩니다. 이러한 모형에서는 관련 상수 추정값도 표시됩니다. 상수 추정값에 대한 정의는 ARIMA 모형 설명 아래에 제공됩니다.
요인
(승법 계절 ARIMA 모형에만 표시됨) 모수를 포함하는 모형의 요인입니다. 승법 계절 모형에서 요인 1은 비계절 요인이고 요인 2는 계절 요인입니다.
시차
(ARIMA 및 계절 ARIMA 모형에만 표시됨) 모수를 곱한 항에 적용되는 시차 또는 후방 연산자의 차수입니다.
추정값
시계열 모형의 모수 추정값입니다.
표준 오차
모수 추정값의 표준 오차 추정값입니다. 이 추정값은 검정 및 예측 구간을 계산하는 데 사용됩니다.
t 비
각 모수가 0이라는 가설에 대한 검정 통계량입니다. 모수에 대한 검정 통계량은 표준 오차에 대한 모수 추정값의 비율입니다. 가설이 참이면 이 통계량은 근사 스튜던트 t 분포를 따릅니다. 절대값이 2보다 큰 t 비는 0.05 유의 수준에 가까우므로 이러한 값을 찾는 것이 유의성을 판단하는 일반적인 규칙입니다.
Prob>|t|
각 모수에 대해 계산되는 관측된 p 값입니다. P 값은 가설이 참일 때 t 비(절대값 기준)가 계산된 값보다 클 확률입니다.
상수 추정값
(절편 또는 평균 항이 포함된 모형에만 표시됨) 상수 추정값에 대한 정의는 ARIMA 모형 아래에 제공됩니다.
평균
(ARIMA 및 계절 ARIMA 모형에만 표시됨) ARIMA 또는 계절 ARIMA 모형의 절편 값에 대한 추정값입니다.
예측
시계열에 대한 관측값과 예측값을 모두 보여 주는 그림입니다. 이 그림은 세로선에 의해 두 영역으로 구분됩니다.
홀드백 집합을 지정한 경우 세로선은 훈련 데이터와 홀드백 데이터를 구분합니다. 세로선 왼쪽에는 1시차 후 예측이 훈련 데이터 점과 중첩됩니다. 세로선 오른쪽에는 모형에서 예측한 값이 홀드백 데이터 점과 중첩됩니다. 예측 구간도 표시됩니다. 플랫폼 시작 창의 "예측 주기" 옵션을 사용하여 예측 값 수를 제어할 수 있습니다.
홀드백 집합을 지정하지 않은 경우 세로선은 관측된 데이터와 미래 예측을 구분합니다. 세로선 왼쪽에는 1시차 후 예측이 관측된 데이터 점과 중첩됩니다. 세로선 오른쪽에는 모형에서 예측한 미래 값과 예측 구간이 표시됩니다. 플랫폼 시작 창의 "예측 주기" 옵션을 사용하거나 "시계열"의 빨간색 삼각형 메뉴에서 "예측 주기 수"를 선택하여 미래 예측 값 수를 제어할 수 있습니다.
잔차
적합 모형을 기반으로 한 잔차 값을 보여 주는 그래프입니다. 이러한 값은 시계열의 관측값에서 1시차 후 예측값을 뺀 값입니다. 잔차에 대한 자기상관 및 편자기상관 보고서도 표시됩니다. 이 보고서를 사용하면 적합 모형이 데이터를 설명하기에 적절한지 여부를 결정할 수 있습니다. 잔차 그림의 점이 0 주위에서 정규 분포를 따르고, 0보다 큰 시차에 대해 잔차의 자기상관 및 편자기상관에 유의한 성분이 없으면 적합 모형이 적절하다고 할 수 있습니다.
홀드백 계열에 대한 예측 오차
(홀드백 집합을 지정한 경우에만 사용 가능) 홀드백 집합의 관측값에 대한 예측 오차 그림입니다. 오차에 대한 자기상관 및 편자기상관 보고서도 표시됩니다.
반복 기록
각 반복에서 목적 함수의 값을 포함합니다. 이 옵션은 적합 절차의 문제를 진단하는 데 유용할 수 있습니다. 데이터에 잘 맞지 않는 모형을 적합시키려고 하면 가능도에 대한 최적값에서 수렴하지 못할 수 있습니다. "반복 기록" 테이블에는 다음과 같은 통계량이 포함됩니다.
반복
반복 번호입니다.
반복 기록
각 단계의 목적 함수 값입니다.
단계
반복 단계의 유형입니다.
목적 함수-기준
목적 함수의 그래디언트 norm입니다.
ARIMA 및 계절 ARIMA 모형 보고서 옵션
각 ARIMA 및 계절 ARIMA 모형 보고서에는 다음 옵션이 포함된 빨간색 삼각형 메뉴가 있습니다.
점 표시
예측 그래프에 데이터 점을 표시하거나 숨깁니다.
예측 구간 표시
예측 그래프에 예측 구간을 표시하거나 숨깁니다.
열 저장
모형 결과를 나타내는 열이 포함된 새 데이터 테이블을 생성합니다.
예측 계산식 저장
(홀드백 집합을 지정한 경우에는 사용 불가능) 데이터 및 예측 계산식을 새 데이터 테이블에 저장합니다.
SAS 작업 생성
SAS에서 모형 분석을 복제하는 SAS 코드를 생성합니다.
잔차 통계량
모형에 대해 나타낼 잔차 통계량의 표시 유형을 제어합니다. 이러한 표시 유형은 시계열 플랫폼 옵션 섹션에서 설명합니다. 그러나 이 설정은 일련의 잔차에 적용됩니다.
적합 제거
보고서에서 개별 모형 적합을 제거합니다.