모형
다음 표에는 파괴 열화 플랫폼의 "경로 정의" 목록에 있는 각 모형에 대한 방정식이 제공됩니다. 각 모형에 대한 설명을 보려면 링크를 클릭하십시오.
참고: 각 방정식의 왼쪽에 표시된 썸네일 스케치는 시간 경과에 따른 위치 모수 m의 동작을 보여 주는 일반 그림입니다. 보고서의 주 그림에 나오는 추정된 중앙값 그림은 "분포" 및 "변환"에서 선택한 옵션에 따라 썸네일과 다를 수 있습니다.
|
모형 |
방정식 |
|---|---|
|
m = b0 + b1 * f(time) |
|
|
m = b1 * f(time) |
|
|
m = b0X + b1 * f(time) |
|
|
m = b0X + b1x * f(time) |
|
|
m = b1X * f(time) |
|
|
m = b0 + b1X * f(time) |
|
|
m = b0 - b1 * Exp[-b2 * Exp[b3 * [Arrhenius(X0) - Arrhenius(X)]] * f(time)] |
|
|
m = b0 * [1 - Exp[-b1 * Exp[b2 * [Arrhenius(X0) - Arrhenius(X)]] * f(time)]] |
|
|
m = b0 + b1 * Exp[-b2 * Exp[b3 * [Arrhenius(X0) - Arrhenius(X)]] * f(time)] |
|
|
m = b0 * Exp[-b1 * Exp[b2 * [Arrhenius(X0) - Arrhenius(X)]] * f(time)] |
|
|
m = b0 ± Exp[b1 + b2 * Arrhenius(X)] * f(time) |
|
|
m = b0 ± Exp[b1 + b2 * Log(X)] * f(time) |
|
|
m = b0 ± Exp[b1 + b2 * X] * f(time) |
변환된 시간에서 선형인 모형
절편을 포함한 공통 경로
이 모형은 변환된 시간에 따라 위치 모수가 선형으로 변하는 단일 분포를 적합시킵니다. 이 모형은 X 변수가 있는지 여부에 관계없이 공통 절편과 공통 기울기를 적합시킵니다.
절편을 포함하지 않은 공통 경로
이 모형은 변환된 시간에 따라 위치 모수가 선형으로 변하지만 시간 0에서의 값이 0인 단일 분포를 적합시킵니다. "분포" 및 "변환"에서 선택한 옵션에 따라 중앙값 곡선이 직선이 아닐 수 있으며 원점을 통과하지 않을 수도 있습니다. 이 모형은 X 변수가 있는지 여부에 관계없이 0 절편과 공통 기울기를 적합시킵니다.
공통 기울기
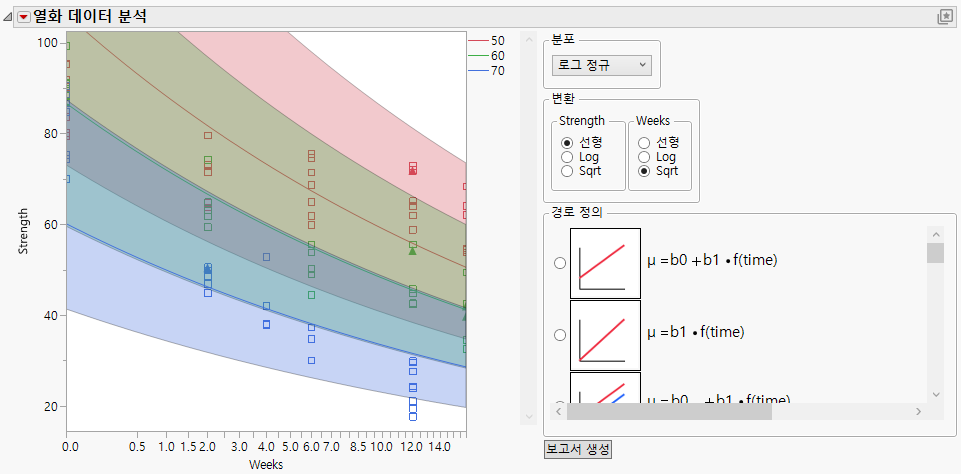
이 모형에서 위치 모수는 변환된 시간의 선형 함수이며, X 값에 대한 개별 절편이 있지만 기울기가 공통입니다. "분포" 및 "변환"에서 선택한 옵션에 따라 모형 적합이 곡선으로 나타날 수 있습니다. 예를 들어 "로그 정규" 분포를 선택하면 Figure 9.12의 그림이 제공됩니다.
그림 9.12 로그 정규 분포를 사용하는 공통 기울기 모형
절편을 포함한 개별 경로
이 모형에서 위치 모수는 변환된 시간의 선형 함수이며, X 값에 대한 개별 절편과 개별 기울기를 갖습니다.
절편을 포함하지 않은 개별 경로
이 모형에서 위치 모수는 변환된 시간의 선형 함수이며, X 값에 대한 0 절편과 개별 기울기를 갖습니다.
공통 절편
이 모형에서 위치 모수는 변환된 시간의 선형 함수이며, X 값에 대한 공통 절편과 개별 기울기를 갖습니다.
1차 운동 역학 모형
위치 모수가 온도의 아레니우스 변환에 기반한 비선형 함수인 네 가지 1차 운동 역학 모형이 제공됩니다. 이러한 각 위치 모형은 선택적 설명 변수 X의 각 값에 대해 개별 모형을 적합시킵니다.
이러한 모형을 처음 선택할 때 온도의 측정 척도와 기준 온도 값 X0을 지정해야 합니다 지정된 기준 온도는 이러한 모형에서 b2의 해석에 영향을 줍니다. b2 모수는 X0에서의 비율 상수입니다. X0 값은 시간 가속 요인을 생성하는 데 사용됩니다(Meeker & Escobar 1998 참조). 이후에 다른 1차 운동 역학 모형 또는 아레니우스 비율 모형(아레니우스 비율 참조)을 선택하면 플랫폼에서 이러한 규격을 기억하고 사용합니다.
1차 운동 역학 유형 1
이 모형에서 b1과 b2는 양수입니다. 선형 척도에서 곡선은 시간이 무한대에 가까워질수록 b0에서 상위 점근선을 갖습니다.
1차 운동 역학 유형 2
이 모형에서 위치 모수는 시간이 0일 때 0입니다. b0과 b1은 모두 양수입니다. 선형 척도에서 곡선은 시간이 무한대에 가까워질수록 b0에서 상위 점근선을 갖습니다. 유형 2 모형은 유형 1 모형의 수직 이동 버전으로 생각할 수 있습니다.
1차 운동 역학 유형 3
이 모형에서 b1과 b2는 모두 양수입니다. b1 앞의 부호가 유형 1 모형에서 b1 앞의 부호와 반대이므로 이 모형은 유형 1 모형의 반전된 버전입니다. 선형 척도에서 시간이 무한대에 가까워질수록 b0에서 하위 점근선을 갖습니다.
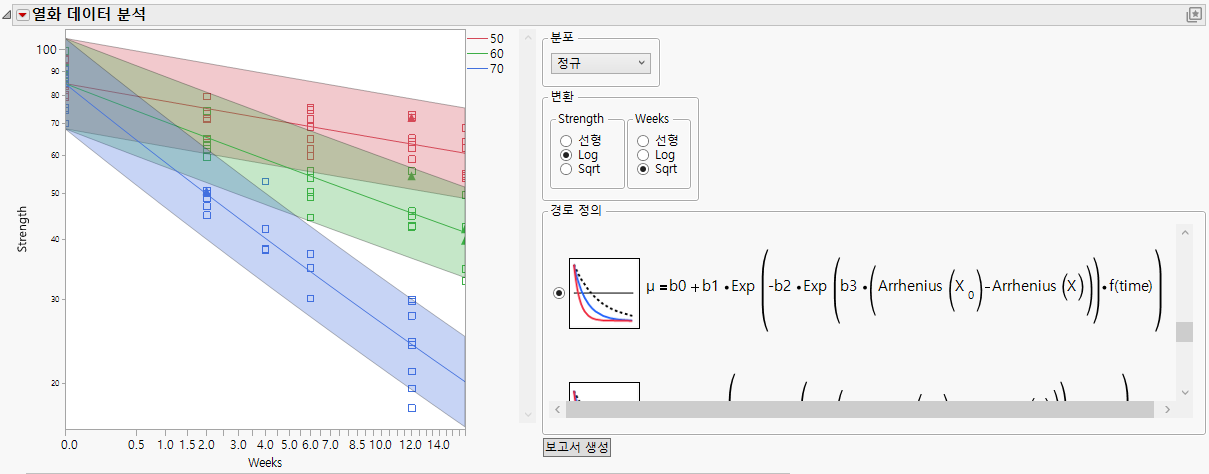
시간 경과에 따라 음의 기울기를 나타내는 데이터가 주어진 경우 적합 모형은 Figure 9.13과 비슷한 그림을 생성할 수 있습니다. 이 그림은 Adhesive Bond.jmp를 사용하여 생성되었습니다. 선택된 온도 측정 척도는 "섭씨"이고 일반 사용 조건에서 지정된 기준 온도는 35도입니다.
그림 9.13 1차 운동 역학 모형 유형 3의 예
1차 운동 역학 유형 4
이 모형은 유형 3 모형의 수직 이동 버전입니다. 선형 척도에서 곡선은 시간이 무한대에 가까워질수록 0에서 하위 점근선을 갖습니다.
비율 모형
위치 모수가 변환된 X 변수의 지수 함수인 세 가지 모형이 제공됩니다. 이러한 각 위치 모형은 선택적 설명 변수 X의 각 값에 대해 공통 절편 및 개별 기울기 모형을 적합시킵니다. 이러한 각 모형의 경우 선형 척도에서 위치 모수는 변환된 시간 값에서 선형입니다.
아레니우스 비율
이 모형은 아레니우스 변환에 변환된 시간을 곱한 지수 함수를 포함합니다. 이 모형을 선택하면 온도의 측정 척도를 지정하라는 메시지가 표시됩니다(이 정보를 아직 제공하지 않은 경우).
다항식 비율
이 모형은 X 로그의 선형 함수에 변환된 시간을 곱한 지수 함수를 포함합니다.
지수 비율
이 모형은 X의 선형 함수에 변환된 시간을 곱한 지수 함수를 포함합니다.