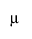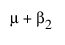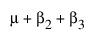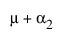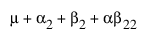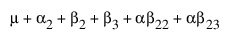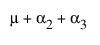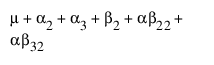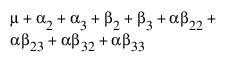순서형 요인
모형 적합 플랫폼에서 순서형 모델링 유형으로 표시된 요인은 명목형 요인과 다르게 코드화됩니다. 모수 추정값이 다르게 해석되고 검정 및 최소 제곱 평균이 다릅니다.
순서형 요인의 첫 번째 수준은 대조 또는 기준 수준이며, 모수는 순서형 요인이 각 후속 수준으로 설정될 때 반응에 미치는 영향을 측정합니다. 순서형 요인 코딩은 첫 번째 용량이 0일 때 다양한 용량을 나타내는 수준이 포함된 요인에 적합합니다. 다음 표에서는 3수준 순서형 요인의 예를 보여 줍니다.
|
항 |
코드화된 열 |
|
|
|
A |
a2 |
a3 |
|
|
A1 |
0 |
0 |
대조 수준, 용량 0 |
|
A2 |
1 |
0 |
낮은 용량 |
|
A3 |
1 |
1 |
높은 용량 |
설계 패턴은 하위 삼각형 요소는 1이고 다른 요소는 0입니다.
단순 주효과 모형의 경우 다음과 같이 지정할 수 있습니다.
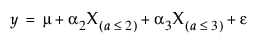
여기서 m는 A = 1에서의 기대 반응, m + a2는 A = 2에서의 기대 반응, m + a2 + a3은 A = 3에서의 기대 반응을 나타냅니다. 따라서 a2는 A = 1에서 A = 2로 이동 효과를 추정하고, a3은 A = 2에서 A = 3으로 이동 효과를 추정합니다.
순서형 주효과에 대한 모든 모수의 부호가 동일하면 순서형 수준에서 반응 효과는 단조 특성을 보입니다.
순서형 교호작용
순서형 교호작용은 명목형 효과와 마찬가지로 요인 열의 수평 직접곱으로 생성됩니다. 두 개의 순서형 요인 A와 B가 있고 각 요인의 수준이 세 개인 경우를 예로 들겠습니다. JMP의 순서형 코딩은 다음에 표시된 설계 행렬을 생성합니다. 교호작용의 패턴은 1로 구성된 하삼각 행렬의 블록 하삼각 행렬입니다.
|
|
|
|
|
|
|
A*B |
|||
|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
A2 |
A3 |
||
|
A |
B |
A2 |
A3 |
B2 |
B3 |
B2 |
B3 |
B2 |
B3 |
|
A1 |
B1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
A1 |
B2 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
A1 |
B3 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
A2 |
B1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
A2 |
B2 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
|
A2 |
B3 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
|
A3 |
B1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
A3 |
B2 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
|
A3 |
B3 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
참고: 효과가 없는지 여부를 검정할 때 단순 모형에 대한 명목형 요인과 순서형 요인 사이에는 큰 차이가 없습니다. 그러나 교호작용이 지정되면 큰 차이를 보입니다. JMP에서는 대부분의 모형에 순서형 요인보다는 명목형 요인을 사용할 것을 권장합니다.
순서형 교차 모형에 대한 가설 검정
모수의 의미를 확인하려면 모수에 관한 셀 평균 기대값을 보여 주는 아래 표를 검토합니다. 여기서 m는 절편, a2는 A2 수준의 모수 등입니다.
|
|
B1 |
B2 |
B3 |
|
A1 |
|
|
|
|
A2 |
|
|
|
|
A3 |
|
|
|
실제로 A에 대한 주효과 검정은 첫 번째 수준에서 B를 포함하는 A 수준을 검정하는 것입니다. 마찬가지로 B에 대한 주효과 검정은 첫 번째 수준에서 A를 포함하는 여러 B 수준의 상단 행을 검정하는 것입니다. 이 검정은 두 요인이 모두 처치 용량이 다른 실험에 적합합니다. 주 관심은 각 처치의 단독 효능이며, 두 약물의 용량을 모두 투여했을 때 약물 교호작용을 찾는 것은 부수적입니다. 경우에 따라 각 약물이 다량 투여되면 위험할 수도 있습니다.
각 셀의 기대값은 현재 행과 열을 포함하여 왼쪽 및 위에 있는 각 셀과 관련된 모든 모수를 더하여 얻을 수 있습니다. 마지막 셀의 기대값은 모든 모수의 합입니다.
다른 효과에 포함된 효과에 대한 가설 검정은 순서형 코딩과 명목형 코딩에서 다르지만 다른 효과에 포함되지 않은 효과를 검정하는 것은 동일합니다. 위의 교차 설계에서 교호작용에 대한 검정은 A와 B의 적합이 명목형인지 아니면 순서형인지에 관계없이 동일합니다.
순서형 최소 제곱 평균
앞에서 설명했듯이 최소 제곱 평균은 다른 모든 요인을 중립 값으로 설정한 후 일부 수준 조합에 해당하는 예측값입니다. JMP는 연관이 없는 순서형 요인이 포함된 효과의 중립 값을 첫 번째 수준(대조 기준 수준)으로 정의합니다.
이와 같은 순서형 요인에 대한 최소 제곱 평균 정의는 포함된 효과의 가설 검정이 최소 제곱 평균의 동일 여부 검정과 동등하다는 개념을 유지합니다.
순서형 효과의 특이성 및 결측 셀
순서형 코딩을 사용하면 순서형 효과의 첫 번째 수준이 기준이라는 것을 의미합니다. 따라서 교호작용에 결측 셀이 있거나 교호작용의 데이터가 없는 경우에도 주효과에 대한 적합한 검정을 얻을 수 있습니다.
결측 셀이 있는 예
이 예는 A3B2 셀에 데이터가 없다는 점을 제외하고 셀당 두 개의 관측값이 있는 위의 예와 동일합니다. 이제 요인의 명목형 코드화 결과를 순서형 코드화 결과와 비교할 수 있습니다. Figure A.2에서 알 수 있듯이 모형 적합은 동일합니다.
|
Y |
A |
B |
|
12 |
1 |
1 |
|
14 |
1 |
1 |
|
15 |
1 |
2 |
|
16 |
1 |
2 |
|
17 |
2 |
1 |
|
17 |
2 |
1 |
|
18 |
2 |
2 |
|
19 |
2 |
2 |
|
20 |
3 |
1 |
|
24 |
3 |
1 |
그림 A.2 명목형 요인(왼쪽) 및 순서형 요인(오른쪽)에 대한 요약 정보
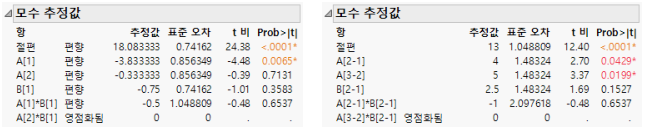
코딩이 다르기 때문에 모수 추정값은 매우 차이가 있습니다. 결측 셀은 명목형 모수의 추정 가능성에 영향을 주지만 순서형 모수에는 영향을 주지 않습니다.
그림 A.3 명목형 요인(왼쪽) 및 순서형 요인(오른쪽)에 대한 모수 추정값
특이성 상세 정보는 선형 종속성을 보여 주며 값을 검토하여 결측 셀을 식별합니다.
그림 A.4 명목형 요인(왼쪽) 및 순서형 요인(오른쪽)에 대한 특이성 상세 정보
명목형에 대한 효과 검정으로 인해 자유도가 손실됩니다. B의 경우 검정이 없습니다. 순서형의 경우 첫 번째 수준(기준)에 대한 결측 셀이 없으므로 손실이 없습니다.
그림 A.5 명목형 요인(왼쪽) 및 순서형 요인(오른쪽)에 대한 효과 검정
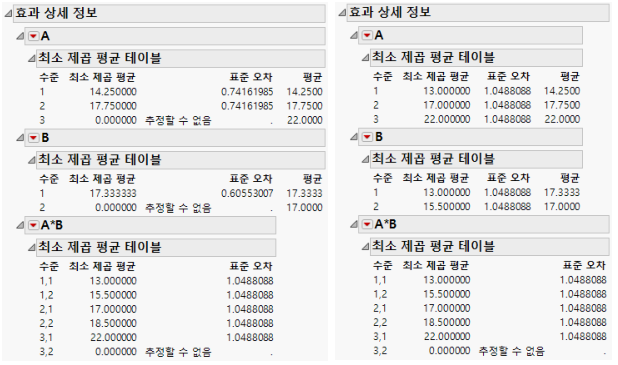
최소 제곱 평균도 다릅니다. 명목형 LSM은 모두 추정 가능한 것은 아니지만 순서형 LSM은 가능합니다. 셀 평균을 검토하여 값을 확인할 수 있습니다. 두 경우에 대한 A*B LSM은 동일합니다. Figure A.6에서는 명목형 요인 및 순서형 요인의 최소 제곱 평균을 보여 줍니다.
그림 A.6 명목형 요인(왼쪽) 및 순서형 요인(오른쪽)에 대한 최소 제곱 평균