 원래 예측 변수에 대한 모수 추정값
원래 예측 변수에 대한 모수 추정값
"일반화 회귀" 보고서의 "원래 예측 변수에 대한 모수 추정값" 섹션에서는 모형의 모든 모수에 대한 추정값 및 기타 결과를 제공합니다. 초기 테이블에는 모형의 예측 변수에 대한 계수가 포함됩니다. 추가 테이블에는 척도, 산포 또는 영과잉 모수와 같은 다른 모형 모수가 포함됩니다. 자세한 내용은 분포 지정에서 확인하십시오. 두 테이블 모두 동일한 결과 열을 포함합니다.
팁: "원래 예측 변수에 대한 모수 추정값" 보고서에서 항을 클릭하여 해 경로 그림에서 해당 경로를 강조 표시할 수 있습니다. 데이터 테이블의 해당 열도 선택됩니다. 이 방법은 추가 분석을 실행할 때 유용합니다. 여러 행을 선택하려면 Shift 키를 누르고 항을 클릭합니다.
"원래 예측 변수에 대한 모수 추정값" 보고서에는 원래(중심화 및 척도화되지 않음) 예측 변수로 표현된 모형의 모수 추정값이 제공됩니다.
이 보고서는 다음 정보를 제공합니다.
항
모형 항 목록입니다. "고급 컨트롤" 옵션을 사용하여 모형에 강제로 적용한 항 옆에는 "강제 적용됨"이 표시됩니다.
추정값
원래 측정값으로 표현된 주어진 모형 항에 해당하는 모수 추정값입니다.
표준 오차
추정값의 표준 오차입니다. 이 값은 M-추정 및 샌드위치 계산식(Zou 2006, Huber and Ronchetti 2009)을 사용하여 구합니다.
t 비 또는 Wald 카이제곱
각 모수의 실제 값이 0인지 여부에 대한 검정 통계량입니다. 지정된 추정 방법이 벌점 회귀 방법이 아니면 정규 분포가 지정되고 중도절단이 지정되지 않으면 "t 비" 열이 나타납니다. 그렇지 않으면 "Wald 카이제곱" 열이 나타납니다. 자세한 내용은 추정 방법 옵션에서 확인하십시오.
Prob>|t| 또는 Prob > ChiSquare
실제 모수 값이 0이라는 검정에 반대되는 양측 대립가설에 대한 p 값입니다. 지정된 추정 방법이 벌점 회귀 방법이 아니면 정규 분포가 지정되고 중도절단이 지정되지 않으면 "Prob>|t|" 열이 나타납니다. 그렇지 않으면 "Prob > ChiSquare" 열이 나타납니다. 자세한 내용은 추정 방법 옵션에서 확인하십시오.
95% 하한
모수에 대한 95% 신뢰 구간의 하한입니다. "모형 적합" 창의 "모형 규격" 빨간색 삼각형 메뉴에서 "유의 수준 설정"을 선택하여 a 수준을 변경할 수 있습니다.
95% 상한
모수에 대한 95% 신뢰 구간의 상한입니다. "모형 적합" 창의 "모형 규격" 빨간색 삼각형 메뉴에서 "유의 수준 설정"을 선택하여 a 수준을 변경할 수 있습니다.
코드화되지 않은 추정값
(모수 추정값 테이블에서 마우스 오른쪽 버튼을 클릭하고 열 > 코드화되지 않은 추정값을 선택한 경우에만 표시됨) 코드화되지 않은 척도로 표시되는 각 항의 모수 추정값입니다. 이 옵션은 "코딩" 열 특성을 포함하는 효과 열이 하나 이상 있고 특정 조건에 해당하는 경우에만 사용할 수 있습니다. 자세한 내용은 코딩 제한에서 확인하십시오.
특이성 상세 정보
(모형 항 사이에 선형 종속성이 있는 경우에만 사용 가능) 모형 항이 충족하는 선형 함수입니다.
VIF
(정규 분포인 경우에만 사용 가능하며, 모수 추정값 테이블에서 마우스 오른쪽 버튼을 클릭하고 열 > VIF를 선택한 경우에만 표시됨) 모형의 각 항에 대한 VIF(분산 팽창 계수)입니다. VIF 값이 높으면 모형의 항 사이에 공선성 문제가 있음을 나타냅니다.
i번째 항 xi의 VIF는 다음과 같이 계산됩니다.
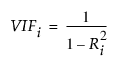
여기서 Ri 2은 다른 설명 변수의 함수로 나타낸 xi 회귀에 대한 R²입니다.