결과 테이블
표지자 주석 위치
표지자의 염색체 위치가 포함된 주석 테이블을 지정한 경우 이 열에 각 표지자의 염색체 위치가 나열됩니다. 위치 정보가 제공되지 않으면 입력 JMP 테이블에서 각 표지자의 열 번호가 대신 나열됩니다.
연계 표지자 주석 위치
표지자의 염색체 위치가 포함된 주석 테이블을 지정한 경우 이 열에 각 비교 표지자의 염색체 위치가 나열됩니다. 위치 정보가 제공되지 않으면 입력 JMP 테이블에서 각 비교 표지자의 열 번호가 대신 나열됩니다.
표지자 쌍 사이의 거리
이 열에는 표지자 쌍 사이의 거리가 나열됩니다. 위치 정보가 제공되지 않으면 입력 JMP 테이블에서 각 비교 표지자 사이의 열 수가 대신 나열됩니다.
개수
각 표지자에 대해 관측된 총 개체 수입니다.
결측 비율
각 표지자 또는 표지자 쌍에 대해 데이터가 결측인 개체의 비율입니다.
유전자형 개수
각 표지자에 대해 관측된 유전자형 개수입니다.
대립유전자 개수
각 표지자에 대해 관측된 대립유전자 개수입니다.
마이너 대립유전자
각 표지자에서 발생 빈도가 낮은 대립유전자입니다.
0으로 코딩된 가장 흔한 대립유전자
각 표지자에서 발생 빈도가 가장 높은 대립유전자입니다. 이 대립유전자에 대한 동형접합 개체는 해당 표지자에 대해 0으로 코딩됩니다.
마이너 대립유전자 빈도(MAF)
MAF는 관측된 모집단에서 각 표지자에 대한 마이너 대립유전자의 비율을 나타냅니다. 대립유전자 M1과 M2를 가진 이중 대립유전자 표지자의 유전자자리를 M으로 가정합니다. 따라서 배수성 k가 짝수인 N개 개체의 표본은 유전자자리에 k + 1개의 다른 유전자형을 가질 수 있습니다. i(i = 0, 1, 2, …, k)개의 M1 대립유전자 복제와 j(j = 0, 1, 2, …, k)개의 M2 대립유전자 복제를 가진 개체 수를 Nij로 표시합니다. M1 대립유전자의 복제 수 n1은 n1 = 0 ´ N00 + 1 ´ N10 + 2 ´ N20 + … + k ´ Nk0 합을 통해 바로 구할 수 있습니다. M1 대립유전자의 표본 빈도는 p1 = n1/(k ´ n), M2 대립유전자의 빈도는 p2 = 1 - p1, M1 대립유전자의 u개 복제와 M2 대립유전자의 v개 복제를 가진 각 유전자형에 대한 표본 빈도는 Pij = Nij/n으로 각각 작성됩니다.
다형성 정보 지수(PIC)
PIC(Botstein et al., 1980; Hilderbrand, Torney, and Wagner, 1992)는 아버지, 어머니, 자녀의 표지자 유전자형을 고려하여 특정 부모가 자녀에게 전달한 대립유전자를 구별할 확률을 측정합니다.
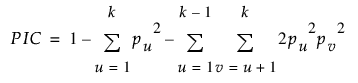
이형접합성(HET)
이형접합성은 관측된 모집단에서 이형접합 개체의 비율을 말하며, 관측 이형접합성이라고도 합니다.
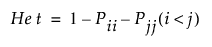
대립유전자 다양성
대립유전자 다양성은 HWE를 유지할 때 데이터 집합에서 이형접합 개체의 기대 비율을 말하며, 기대 이형접합성이라고도 합니다.
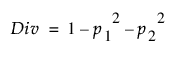
HWE 자유도
HWE 자유도는 
계산식을 사용하여 계산됩니다. 여기서 k는 테스트 중인 특정 표지자에 대해 발견된 대립유전자 수입니다.
HWE 카이제곱
이상적인 모집단 조건을 가정할 때 한 개체가 각 부모로부터 하나씩 받는 두 개의 대립유전자는 서로 독립적이므로 Pii = p12, Pjj = p22, Pij = 2p1 p2 (i, j = 0, 1, 2, …, k)입니다.
이형접합체의 인수 2는 일반적으로 M1/M2 유전자형과 M2/M1 유전자형을 구별할 수 없다는 사실을 인정합니다. 유전자자리 내의 대립유전자 독립성에 대한 이 견해를 HWE(Hardy-Weinberg 평형)라고 합니다. 선택, 돌연변이, 인구 이동 또는 선택적 교배 등의 요인으로 인해 HWE에서의 일탈이 발생할 수 있습니다. 카이제곱 적합도 검정을 사용하여 표지자의 HWE 상태를 검정할 수 있습니다(귀무가설: Pii = p12, Pjj = p22, Pij = 2p1 p2).
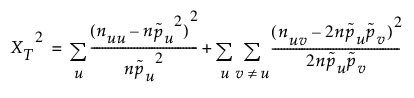
LD 카이제곱(ChiSQLD)
카이제곱 통계량은 CLD(복합 연관비평형) 계수(Weir 1979)를 사용하여 연관비평형 측도의 강도를 추정합니다. 이 방법은 HWE 가정이 필요하지 않으며 대립유전자 빈도와 두 유전자자리의 유전자형 빈도만 사용합니다.
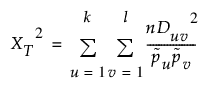
이중 대립유전자 표지자의 경우 k와 l = 2이며 이 검정의 자유도는 1입니다.
복합 LD(D)
HWE를 가정하지 않는 CLD(복합 연관비평형) 계수(Weir 1979)의 측도이며 D12 = p12 + p1/2 - 2p1 p2로 작성됩니다. 다음은 각 요소에 대한 설명입니다.
– p12는 배우자 M1 M2의 빈도입니다.
– p1/2는 서로 다른 두 배우자에서 대립유전자 M1과 M2의 결합 빈도입니다.
– p1과 p2는 두 유전자자리에서 대립유전자 M1과 M2의 빈도입니다(Weir 1996).
표준화 복합 LD(D’)
Dmax에 대한 D의 비율입니다(Zaykin, 2004).
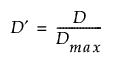
LD 상관계수(r)
두 유전자자리의 존재를 나타내는 표시 변수를 -1에서 1 사이의 값으로 가정한 상관계수입니다.
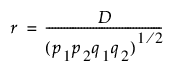
p 값 연관 측도
p 값, LogWorth(log10 p 값), FDR p 값(False Discovery Rate p 값) 및 FDR LogWorth라는 p 값 관련 열이 4개 있습니다. 이 값은 Hardy-Weinberg 평형 및/또는 연관비평형에 대한 카이제곱 검정의 강도를 나타내는 측도입니다.