고급 방법에 대한 통계 상세 정보
이 섹션에는 주성분 시작 창에서 "고급"을 "방법 유형"으로 지정한 경우 사용되는 추정 방법에 대한 통계 상세 정보가 포함되어 있습니다. 이러한 방법은 SVD(특이값 분해)를 기반으로 합니다. 이 알고리즘은 공분산 행렬을 계산하지 않으므로 계산이 효율적입니다.
완전 SVD
완전 SVD 방법은 행렬의 완전 특이값 분해를 기반으로 하는 알고리즘을 사용합니다. 다음 표기를 고려하십시오.
• n = 행 수
• p = 변수 수
• X = 데이터 값의 n x p 행렬
0이 아닌 고유값 수와 이에 따른 주성분 수는 X의 상관 행렬 계수와 같습니다. 0이 아닌 고유값 수는 n과 p 중 더 작은 값을 초과할 수 없습니다.
데이터는 완전 SVD 방법을 구현하기 전에 표준화됩니다. 값을 표준화하려면 평균을 뺀 후 표준편차로 나눕니다. 표준화된 데이터 값의 n x p 행렬을 Xs로 나타냅니다. 그러면 표준화된 데이터의 공분산 행렬은 X의 상관 행렬이며 다음과 같이 정의됩니다.
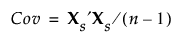
특이값 분해를 사용하면 Xs가 UDiag(L)V¢로 표기됩니다. 이 표현은 Xs¢Xs의 고유 벡터 및 고유값을 얻는 데 사용됩니다. 주성분 또는 스코어는 XsV로 제공됩니다. 추가 배경 정보는 와이드 선형 방법 및 특이값 분해에서 확인하십시오.
절단 SVD
절단 SVD 방법은 특이값 분해를 기반으로 하지만 완전 분해를 구현하지 않는 알고리즘을 사용합니다. 대신 이 알고리즘은 특이값 분해에서 첫 번째 지정한 수의 특이값과 특이 벡터만 계산합니다. 따라서 첫 번째 지정한 수의 고유값과 주성분만 반환됩니다. 이 알고리즘에 대한 자세한 내용은 Baglama와 Reichel(2005) 연구 자료에서 확인하십시오.
랜덤화 SVD
랜덤화 SVD 방법은 특이값 분해를 기반으로 하지만 완전 분해를 구현하지 않는 알고리즘을 사용합니다. 이 알고리즘은 낮은 계수 행렬 근사를 포함하는 2단계 프로세스입니다. 일반적으로 낮은 계수 행렬 근사의 목표는 k가 p보다 훨씬 작고 A » BC가 되도록 m ´ k 행렬 B와 k ´ p 행렬 C를 찾아 m ´ p 행렬 A에 근사한 값을 산출하는 것입니다.
완전 SVD에 설명된 것과 동일한 표기를 고려하십시오. 여기서 목표는 Xs를 분해하는 것입니다.
랜덤화 SVD 알고리즘의 첫 번째 단계에서는 다음 조건을 충족하는 행렬 Q를 찾습니다.
• Q에 l개의 직교정규 열이 있음(k £ l £ p)
• Xs » QQ¢Xs
가능한 한 적은 수의 열이 있는 Q를 효율적으로 계산하기 위한 상세 정보는 Halko, Martinsson & Tropp(2011)에서 확인하십시오.
알고리즘의 두 번째 단계에서는 Q를 사용하여 Xs의 특이값 분해를 계산합니다. B = Q¢Xs라고 하면 다음 조건을 충족합니다.
B = Q¢Xs Þ QB = QQ¢Xs Þ QB = Xs
그런 다음 B의 SVD를 계산합니다(Xs보다 훨씬 작음).
B » U*Diag(L)V¢
QB » (QU*)Diag(L)V¢
A » UDiag(L)V¢, 여기서 U = QU*
완전 랜덤화 SVD 알고리즘에 대한 자세한 내용은 Halko, Martinsson & Tropp(2011)에서 확인하십시오.