변수 중요도 평가에 대한 통계 상세 정보
이 섹션에는 예측 프로파일러의 변수 중요도 지수 계산 방법과 관련된 상세 정보가 포함되어 있습니다.
배경
예측 모형을 나타내는 함수를 f로 표시하고 x1, x2, ..., xn을 모형의 요인 또는 주효과로 가정합니다. y = f(x1, x2 ..., xn)이라고 하겠습니다.
• y의 기대값 E(y)는 x1, x2, ..., xn의 결합 분포에 대해 y를 적분하여 정의됩니다.
• y의 분산 Var(y)는 x1, x2, ..., xn의 결합 분포에 대해 (y – E(y))2을 적분하여 정의됩니다.
주효과
주효과 xj가 y에 미치는 영향은 Var(E(y |xj))로 설명할 수 있습니다. xj가 주어지면 x1, x2, ..., xn의 조건부 분포와 관련하여 기대값을 구하고 xj의 분포에 분산이 전달됩니다. 즉, Var(E(y |xj))는 xj가 고정된 경우 y의 평균에서 xj의 분포에 대한 변동을 측정합니다.
결과적으로 Var(E(y |xj))/Var(y) 비율은 xj 요인에 대한 y의 민감도를 나타내는 측도입니다. "요약 보고서"에서 "주효과" 열의 중요도 지수는 이 비율의 추정값입니다. 자세한 내용은 표집 변동 조정에서 확인하십시오.
총 효과
"총 효과" 열은 xj를 포함하는 모든 항에서 y = f(x1, x2 ..., xn)의 분산에 대한 총 기여도를 나타냅니다. 총 효과 계산은 함수 분해의 개념을 사용합니다. 함수 f는 단일 변수, 변수 쌍 등의 효과를 나타내는 함수와 상수의 합으로 분해됩니다. 이러한 성분 함수는 주효과, 교호작용 효과 및 고차 효과와 비슷합니다. 자세한 내용은 Saltelli(2002), Sobol(1993)에서 확인하십시오.
xj가 들어 있는 항이 포함된 성분 함수가 식별됩니다. 이러한 각 함수에 대해 조건부 기대값의 분산이 계산됩니다. 그런 다음 이러한 분산이 합산됩니다. 합계는 xj를 포함하는 항에 기인한 Var(y)에 대한 총 기여도를 나타냅니다. 각 xj에 대해 이 합계는 입력 생성을 위해 선택된 방법을 사용하여 추정됩니다. "총 효과" 열에 보고된 중요도 지수는 이러한 추정값입니다. 자세한 내용은 표집 변동 조정에서 확인하십시오.
x1과 x2라는 두 개의 요인이 있는 간단한 예를 가정해 보겠습니다. 이 경우 x1에 대한 총 효과 중요도 지수는 다음 식의 추정값입니다.
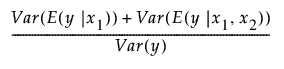
표집 변동 조정
요약 테이블에 표시된 주효과 및 총 효과 추정값은 표집 방법을 사용하여 계산되므로 값이 조정되었을 수 있습니다. 구체적으로 말하면 총 효과 추정값이 주효과 추정값보다 작은 경우 총 효과 중요도 지수는 주효과 추정값과 동일하게 설정됩니다. 주효과 추정값의 합이 1을 초과할 경우 이러한 추정값은 합이 1이 되도록 정규화됩니다.
변수 중요도 표준 오차
독립 입력에 대해 제공되는 표준 오차는 몬테카를로 반복의 정확도를 측정합니다. 중요도 지수는 다음과 같이 계산됩니다.
• 라틴 초입방체 표집을 사용하여 데이터 값 집합을 생성합니다.
• 각 데이터 값 집합에 대해 주효과 및 총 효과 중요도 추정값이 계산됩니다.
• 이 과정은 모든 요인에 대한 주효과 및 총 효과 중요도 지수의 추정 표준 오차가 임계값 0.01 미만이 될 때까지 반복됩니다.
보고되는 표준 오차는 반복이 종료될 때 유효한 표준 오차 값입니다.