경쟁 원인에 대한 통계 상세 정보
경쟁 원인 모형의 경우 집계 분포에 대한 닫힌 형식은 다음과 같이 정의됩니다.
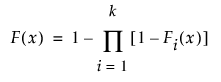
여기서, Fi(x), i = 1, ¼, k는 원인에 해당하는 개별 고장 분포입니다. 관련된 모든 추정값이 MLE이므로 신뢰 한계를 쉽게 구할 수 있습니다.
고정 모수 모형을 원인에 대한 분포로 지정
원인에 대해 고정 모수 모형을 지정한 경우 해당 원인의 "개별 원인" 보고서에서 모수를 고정해야 합니다. "수명 분포 - 고장 원인: <이름>" 보고서의 원하는 "모수 추정값" 보고서에서 모수를 고정합니다. "모형 업데이트"를 클릭하면 고정 모수가 집계 분포에 포함됩니다.
이 예에서는 고정 모수 모형을 집계 분포에 포함하는 방법을 보여 줍니다.
1. 도움말 > 샘플 데이터 폴더를 선택하고 Reliability/Appliance.jmp를 엽니다.
2. 분석 > 신뢰성 및 생존 > 수명 분포를 선택합니다.
3. Time Cycles를 선택하고 Y, 사건 발생 시간을 클릭합니다.
4. Cause Code를 선택하고 고장 원인을 클릭합니다.
5. 고장 모드에서 고정 모수 모형을 사용하도록 허용을 선택합니다.
6. 확인을 클릭합니다.
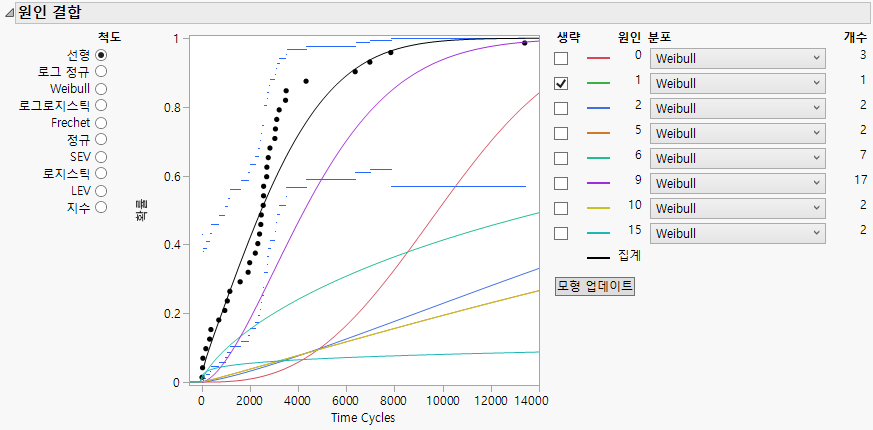
그림 3.25 원인 1이 생략된 고정 모수 모형
데이터가 충분하지 않아 원인 = 1이 기본적으로 생략되었습니다. 그러나 이 원인을 생략하고 싶지 않습니다.
7. 원인 1에 대한 "개별 원인" 보고서를 엽니다. 이 보고서 이름은 "수명 분포 - 고장 원인: 1 고장 개수: 1"입니다.
8. "모수 추정값 - Weibull" 옆의 빨간색 삼각형을 클릭하고 모수 고정을 선택합니다.
9. Weibull 베타를 선택하고 "2"를 입력합니다.
10. 업데이트를 클릭합니다.
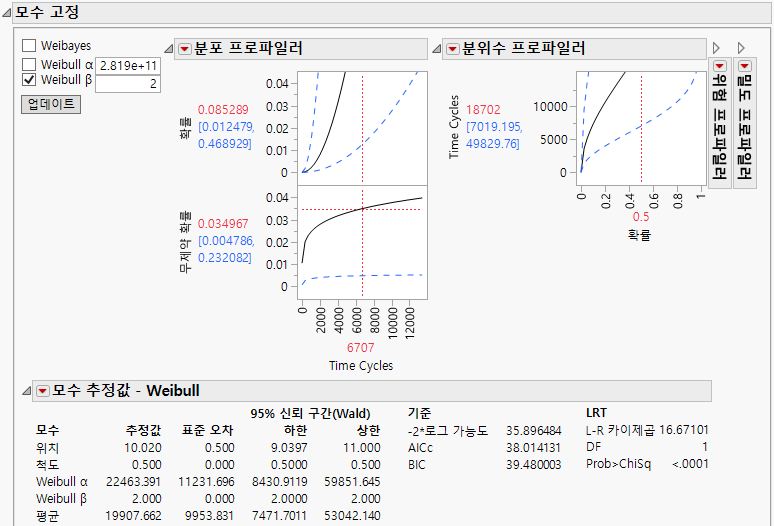
그림 3.26 Weibull 베타가 지정된 고정 모수 모형
"모수 추정값 - Weibull" 보고서에서 b를 2라고 가정하면 알파 모수는 22463.391로 추정됩니다. 이제 원인=1에 대한 고장 분포에 이 값을 사용할 수 있습니다.
11. 보고서 창 맨 위의 "원인 결합"이 나올 때까지 위로 스크롤합니다.
12. 원인 1에 대한 생략을 선택 취소합니다.
13. 원인 1에 대한 분포에서 고정 모수 Weibull을 선택합니다.
14. 모형 업데이트를 클릭합니다.
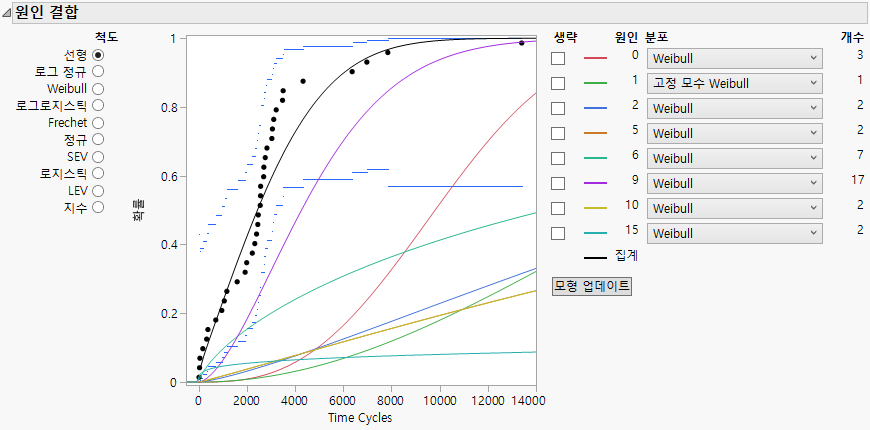
그림 3.27 원인 1을 보여 주는 업데이트된 모형
이제 집계 모형은 전체 경쟁 원인 모형에서 원인 1에 대한 고정 모수 Weibull 결과를 사용합니다.
원인에 대한 베이지안 모형 지정
원인에 대한 베이지안 모형을 지정하는 단계는 고정 모수 모형을 원인에 대한 분포로 지정에 설명된 단계와 비슷합니다. 개별 원인에 대한 수명 분포 보고서의 "통계량"에 있는 해당 "모수 추정값" 개요의 "베이지안 추정" 보고서에서 모형을 정의합니다. 자세한 내용은 베이지안 추정 - <분포 이름>에서 확인하십시오.
베이지안 모형을 집계 모형에 포함하려면 다른 원인에 대한 비베이지안 분포가 시뮬레이션 기반 프레임워크에 적합해야 합니다. 예를 들어 모형에 두 개의 고장 원인이 있다고 가정해 보겠습니다. 하나는 Weibull 분포를 사용하여 모델링되고, 다른 하나는 두 번째 Weibull의 모수를 추정하기 위해 베이지안 방법을 사용하여 모델링됩니다. 첫 번째 Weibull 분포에서 벡터 q1로 표시되는 모수는 최대 가능도를 사용하여 추정됩니다. 두 번째 Weibull의 모수 q2는 베이지안 방법을 사용하여 추정됩니다.
F(x, q1, q2)로 표시되는 집계 혼합 분포의 분위수와 중앙값은 다음과 같이 구합니다.
• 첫 번째 Weibull에 대해 모수 붓스트랩이 수행되어 최대 가능도 추정값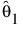 
의 점근 분포에서 랜덤 표본을 생성합니다. 
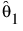의 점근 분포에서 표집된 값을 
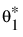로 나타냅니다.
• q2의 사후 분포에서 표본이 추출되고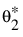 
로 나타냅니다.
• 
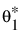및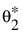 
값의 각 집합에 대해 F*(x, q1, q2)로 표시되는 F(x, q1, q2)의 추정값을 구합니다.
• F*(x, q1, q2) 값을 사용하여 집계 분포의 분위수 및 중앙값에 대한 추정값을 구합니다. 이러한 값은 분포 프로파일러에서 주어진 x 값에 대해 표시됩니다.
원인에 대한 Weibayes 모형 지정
원인에 대한 Weibayes 모형을 지정하는 단계는 고정 모수 모형을 원인에 대한 분포로 지정에 설명된 단계와 비슷합니다. 원인에 대한 수명 분포 보고서의 "통계량"에서 "모수 추정값 - Weibull" 개요에 있는 "모수 고정" 옵션을 선택합니다. "모수 고정" 보고서에서 "Weibayes" 옵션을 선택합니다. Weibayes 모형은 베이지안 모형으로 처리되고 알파 모수의 사후 분포에서 붓스트랩 표본이 추출됩니다. 자세한 내용은 Liu & Wang(2013)에서 확인하십시오.
평균 잔존 수명 계산기
"평균 잔존 수명 계산기"의 빨간색 삼각형 메뉴에 있는 "구성" 옵션을 사용하여 평균 잔존 수명 계산에 사용되는 시뮬레이션된 고장 시간 수의 값을 설정합니다. 이 값을 m으로 표시합니다.
시간 t에서의 평균 잔존 수명 추정값을 구하기 위해 시간 t까지의 생존을 조건으로 하는 집계 분포에서 m개의 표본이 추출됩니다. 이에 대해 평균이 계산됩니다.
평균 잔존 수명에 대한 신뢰 한계를 계산하려면 "구성" 창에서 상자를 선택해야 합니다. 그런 다음 붓스트랩 표본 수를 설정할 수 있습니다. 이 값을 n으로 표시합니다.
신뢰 구간을 계산하기 위해 MLE의 점근 분포에서 또는 베이지안 추론을 사용하여 파생된 사후 분포에서 모수 추정값의 n개 표본이 추출됩니다. 모수 값의 각 표본에 대해 집계 분포가 구성되며, 여기서 평균 잔존 수명 계산을 위한 m개의 표본이 추출됩니다. n개의 평균 잔존 수명 값 표본을 사용하여 신뢰 구간이 생성됩니다.
혼합 적합의 예측 계산식 저장
이 섹션에서는 혼합 적합 보고서의 "예측 저장" 옵션으로 저장된 열의 값을 계산하는 데 사용되는 계산식을 제공합니다.
다음 표기를 고려하십시오.
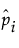- 혼합 비율 wi의 추정값
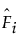- Fi의 추정된 확률 분포 함수
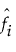- Fi의 추정된 확률 밀도 함수
• 관측값 y가 중도절단되지 않은 경우 저장된 값은 다음 식으로 계산됩니다.
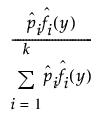
• 관측값이 중도절단된 경우 저장된 값은 중도절단되지 않은 관측값에 대한 계산식의 추정 밀도 값을 다음으로 대체하여 계산됩니다.
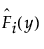오른쪽 중도절단의 경우
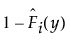왼쪽 중도절단의 경우
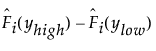구간 중도절단의 경우