직접 모형 적합에 대한 통계 상세 정보
함수 데이터 탐색기 플랫폼의 직접 모형 적합은 행렬 분해에 의존합니다. 데이터가 쌓인 행렬 형식으로 변환됩니다. 행렬의 각 행은 ID 변수의 한 수준에 대한 전체 출력 함수에 해당하고 행렬의 각 열은 입력 변수의 수준에 해당합니다. 직접 모형은 쌓인 함수 행렬에 대해 몇몇 유형의 행렬 분해 루틴을 수행하여 FPCA(함수 주성분 분석) 결과를 얻습니다. 여러 직접 방법에서 사용되는 행렬 분해 중 하나는 SVD(특이값 분해)입니다.
n x p 행렬 X에 대한 SVD를 다음과 같이 쓸 수 있습니다.
X » UDV¢
U, D 및 V 행렬은 다음과 같은 특성을 가집니다.
• U는 U¢U = Ir인 n x r 스코어 직교 행렬입니다.
• V는 V¢V = Ir인 p x r 적재 직교 행렬입니다.
• D는 sk로 나타내는 양수 특이값의 r x r 대각 행렬입니다.
• r << min(n, p)
V의 열은 형상 함수에 해당하고 특이값은 고유값에 해당합니다. 데이터의 각 함수는 형상 함수(V의 열)의 선형 결합을 사용하여 근사값을 산출할 수 있습니다.
벌점 SVD
벌점 SVD 방법은 쌓인 함수 행렬을 한 번에 한 차원씩 분해합니다. SVD(특이값 분해) 방법에서 이는 X의 계수 1 최적 근사를 찾는 것을 의미합니다. X의 계수 1 근사값을 산출하는 것은 제곱 Frobenius norm을 최소화하는 것과 같으며 다음과 같이 쓸 수 있습니다.
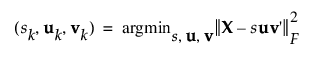
벌점 모수를 통합한 후 최소화 함수는 다음과 같이 작성됩니다.
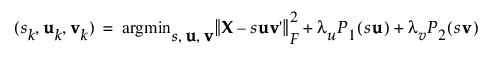
여기서 P1(su)과 P2(sv)는 희소성을 유도하는 벌점 모수입니다.
각 차원 k에 대해 다음 루틴이 수행됩니다.
1. 표준 SVD를 수행하여 시작 값을 구합니다.
2. u를 고정하고 Lasso 벌점을 적용한 벌점 회귀를 수행하여 v의 해를 구합니다(AICc 검증 사용).
3. v를 고정하고 Lasso 벌점을 적용한 벌점 회귀를 수행하여 u의 해를 구합니다(AICc 검증 사용).
4. u와 v가 수렴할 때까지 step 2와 step 3를 반복합니다.
자세한 내용은 Lee et al(2010)에서 확인하십시오.
비음 SVD
비음 SVD 방법은 다음과 같은 추가 제약 조건을 적용하여 쌓인 함수 행렬에 대해 SVD(특이값 분해)를 수행합니다.
X » UDV¢ 여기서 Uij ³ 0, Vij ³ 0
이 방법은 제약된 최소 제곱을 사용하여 U와 V의 해를 구합니다.
다변량 곡선 해상도
MCR(다변량 곡선 해상도) 방법도 행렬 분해를 사용하지만 쌓인 함수 행렬을 세 개가 아니라 두 개의 행렬로 분해합니다. n x p 행렬 X에 대한 행렬 분해를 다음과 같이 쓸 수 있습니다.
X » CS¢
C 및 S 행렬은 다음과 같은 특성을 가집니다.
Cij ³ 0
Sij ³ 0
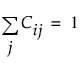, C의 각 행의 합 = 1
S의 열은 비음 형상 함수이고 C의 행은 혼합 비율입니다. 이렇게 하면 각 개별 함수에 대해 스코어의 합이 1이고 함수가 형상 함수의 혼합인 X의 근사가 생성됩니다.