용해 곡선 분석에 대한 통계 상세 정보
이 섹션에는 곡선 적합 플랫폼의 모형 없는 용해 분석에 사용되는 요인을 계산하기 위한 계산식이 포함되어 있습니다. 이 계산식에서는 다음과 같은 표기를 사용합니다.
mRi는 ti 시점에서 대조 곡선 배치에 대한 용해 값의 평균입니다.
mTi는 ti 시점에서 시험 곡선 배치에 대한 용해 값의 평균입니다.
i = 1, ..., N은 시점 수입니다.
F1 차이 요인
F1 차이 요인은 각 시점에서 대조 정제의 곡선과 시험 정제의 곡선 간 차이 비율을 측정합니다. F1은 다음 계산식을 사용하여 계산됩니다.
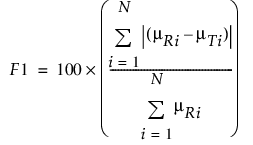
F2 유사성 요인
F2 유사성 요인은 대조 정제의 곡선과 시험 정제의 곡선 간 용해 비율 유사성을 측정합니다. F2는 다음 계산식을 사용하여 계산됩니다(Paixão et al. 2017 참조).
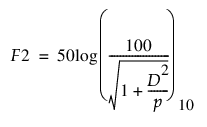
다음은 각 요소에 대한 설명입니다.
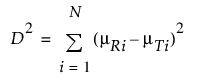
p - 시점 수
Mahalanobis 거리
Mahalanobis 거리 M은 대조 정제의 곡선과 시험 정제의 곡선 간 다변량 거리를 측정합니다. M은 다음 계산식을 사용하여 계산됩니다(Paixão et al. 2017 참조).
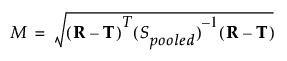
다음은 각 요소에 대한 설명입니다.
R = [mR1,...,mRN]T
T = [mT1,...,mTN]T
Spooled = (SR + ST)/2
SR = 대조 곡선 값의 공분산 행렬
ST = 시험 곡선 값의 공분산 행렬
10% 최대 차이는 다음 계산식을 사용하여 계산됩니다.
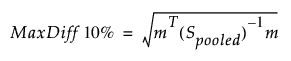
여기서 m은 10의 Nx1 벡터입니다.
T2EQ
Wellek T2EQ 방법의 검정 통계량 T2은 Mahalanobis 거리에서 계산된 Mahalanobis 거리 M을 사용합니다.
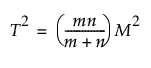
다음은 각 요소에 대한 설명입니다.
m = 대조 정제의 곡선 수
n = 시험 정제의 곡선 수
M = Mahalanobis 거리
검정 통계량은 비중심 F 분포를 따릅니다. 검정 통계량의 p 값은 다음 계산식을 사용하여 계산됩니다(Hoffelder 2019).
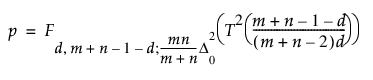
다음은 각 요소에 대한 설명입니다.
Fs1, s2; nc(x) = 비중심 F 분포에 대한 누적 밀도 함수
d = 연구의 시점 수
D20 = 차이 마진
이 계산식에서는 차이 마진 10을 사용합니다.