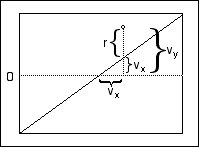
레버리지 그림에 대한 통계 상세 정보
모형 적합 플랫폼의 표준 최소 제곱 분석법은 레버리지 그림을 생성합니다. 이 그림은 편회귀 잔차 레버리지 그림(Belsley et al. 1980) 또는 추가 변수 그림(Cook and Weisberg 1982)이라고도 합니다. Sall(1990)에서는 이러한 그림을 선형 가설에 적용하도록 일반화했습니다.
JMP에서는 다음과 같은 두 가지 유형의 레버리지 그림을 제공합니다.
• 효과 레버리지 그림에는 다른 모든 효과가 모형에 있을 때 해당 효과가 모형에 없다는 가설을 기준으로 관측값이 표시됩니다.
• "실제값 대 예측값 그림" 보고서에 나오는 전체 모형 레버리지 그림에는 요인 효과가 없다는 가설을 기준으로 관측값이 표시됩니다.
효과 레버리지 그림에서는 하나의 효과만 0으로 가정됩니다. 그러나 전체 모형에 대한 실제값 대 예측값 그림에서는 모든 효과가 0으로 가정됩니다. Sall(1990)에서는 레버리지 그림의 개념을 임의의 선형 가설로 일반화하며, 전체 모형 레버리지 그림이 그 예입니다. 이 섹션에 요약된 해당 연구 자료의 상세 정보는 JMP에 있는 두 가지 유형의 그림에 특화되어 있습니다.
생성
추정 가능한 관심 가설이 다음과 같다고 가정해 보겠습니다.
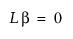
레버리지 그림은 각 점에서 경사진 회귀선까지의 거리가 무제약 잔차를 표시하도록 점을 그려 이 검정의 특징을 나타냅니다. 0에서 수평선까지의 거리는 적합이 가설의 제약을 받을 때 잔차를 표시합니다. 이 두 잔차 집합의 제곱합 간의 차이는 가설로 인한 제곱합입니다. 이 값은F-검정의 주성분이 됩니다.
가설의 제약을 받는 모수 추정값을 다음과 같이 작성할 수 있습니다.
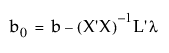
여기서 b는 최소 제곱 추정값입니다.
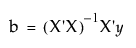
람다는 가설 제약 조건에 대한 라그랑즈 승수이며 다음과 같이 계산됩니다.
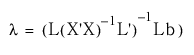
무제약 잔차와 가설의 제약을 받는 잔차는 각각 다음과 같습니다.
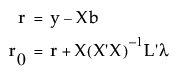
각 관측값에 대해 가로 축 값이 vx이고 세로 축 값이 vy인 점을 가정해 보겠습니다. 다음은 각 요소에 대한 설명입니다.
• vx는 제약된 잔차에서 무제약 잔차를 뺀 r0 - r이며, 제약 조건이 적용된 후 남은 정보를 반영합니다.
• vy는 가로 축 값에 무제약 잔차를 더한 값입니다.
따라서 이 점의 x 및 y 좌표는 다음과 같습니다.
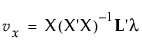및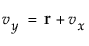 
이러한 점을 기반으로 레버리지 그림이 생성됩니다. Figure 3.51에서는 평균 반응이 0이고 실선 기울기가 1인 레버리지 그림 생성 구조를 보여 줍니다.
JMP의 레버리지 그림에는 반응 평균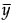 
에 수평 점선이 있습니다. 그림에 표시된 점은 (vx +
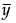, vy)로 지정됩니다.
그림 3.51 레버리지 그림 생성
레버리지 그림에 검정 중첩
단순 선형 회귀에서 반응 기대값에 대한 신뢰 한계를 예측 변수 x의 평활 함수로 그림에 표시할 수 있습니다.
Upper(x) =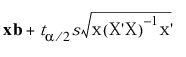 
Lower(x) =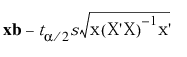 
여기서 x = [1 x]는 예측 변수의 2-벡터입니다.
Figure 3.40에 표시된 것처럼 이러한 신뢰 곡선을 통해 해당 가설 검정의 유의성을 시각적으로 평가할 수 있습니다.
• 유의함: 기울기 모수가 0과 유의한 차이가 있으면 신뢰 곡선이 반응 평균에서 수평선과 교차합니다.
• 경계선: 기울기 모수에 대한 t-검정이 유의성 한계에 있으면 신뢰 곡선이 반응 평균에서 수평선에 점근적입니다.
• 유의하지 않음: 기울기 모수가 0과 유의한 차이가 없으면 신뢰 곡선이 반응 평균에서 수평선과 교차하지 않습니다.
레버리지 그림은 신뢰 곡선을 표시하여 이 개념을 반영합니다. 그림이 적절하게 중앙에 오도록 조정됩니다. 가로 축의 점을 z로 나타냅니다. 함수를 다음과 같이 정의합니다.
Upper(z) =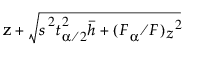 
및
Lower(z) =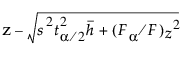 
여기서 F는 가설에 대한 F 통계량이고 Fα는 유의 수준 a에 대한 참조 값입니다.
또한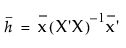 
입니다. 여기서 
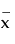는 예측 변수에 대한 적절한 중간 값(예: 평균)으로 구성된 행 벡터입니다.
이러한 함수는 다음과 같이 단순 선형 회귀에 대한 신뢰 곡선과 동일한 방식으로 작동합니다.
• F 통계량이 참조 값보다 크면 신뢰도 함수가 가로 축과 교차합니다.
• F 통계량이 참조 값과 같으면 신뢰도 함수의 가로 축이 점근선으로 표시됩니다.
• F 통계량이 참조 값보다 작으면 신뢰도 함수가 교차하지 않습니다.
또한 Upper(z) - Lower(z)가 z에서의 예측값에 대한 유효한 신뢰 구간이어야 합니다.
참고: 일부 모형의 경우 레버리지 그림의 신뢰 구간에 대한 추가 척도화가 수행됩니다. 이 척도화는 모형과 모형의 복잡성에 따라 달라집니다.