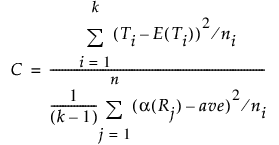비모수 검정 통계량에 대한 통계 상세 정보
이 섹션에서는 일원 분석 플랫폼의 Wilcoxon, 중앙값, van der Waerden 및 Friedman 순위 검정에 사용되는 검정 통계량의 계산식을 제공합니다.
표기
언급된 검정은 스코어를 기반으로 하며 다음과 같은 표기를 사용합니다.
j = 1,..., n
전체 표본의 관측값입니다.
i = 1,..., k
X의 수준입니다. 여기서 k는 총 수준 수입니다.
n1, n2,..., nk
X의 k개 수준 각각에 포함된 관측값의 개수입니다.
Rj
j번째 관측값의 중간 순위입니다. 중간 순위는 해당 관측값의 순위(동일 점수가 없는 경우)이거나 평균 순위(동일 점수가 있는 경우)입니다.
a
다양한 검정에서 스코어를 정의하는 데 사용되는 중간 순위의 함수입니다.
시작 창에서 블록 변수를 지정한 경우에는 다음 표기가 사용됩니다.
b = 1,..., B
블록 변수의 수준입니다. 여기서 B는 총 블록 수입니다.
Rbi
블록 b 내에 있는 X의 i번째 수준에 해당되는 중간 순위입니다.
함수 a는 스코어를 다음과 같이 정의합니다.
Wilcoxon 스코어
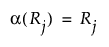
중앙값 스코어
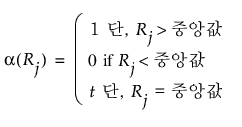
nt가 중앙값 위치에 있는 동일 관측값의 개수이고, nu이 중앙값보다 큰 관측값의 개수라고 할 때, t는 다음과 같이 구합니다.

van der Waerden 스코어

Friedman 순위 스코어
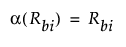
2표본 정규 근사
정규 근사를 기반으로 하는 검정은 X의 수준이 정확히 두 개뿐인 경우에만 가능합니다. 이 섹션에서 사용되는 표기는 표기에 정의되어 있습니다. 2표본 정규 근사 보고서에 표시되는 통계량은 아래와 같이 정의됩니다.
S
통계량 S는 더 작은 그룹에 있는 관측값에 대한 a(Rj) 값의 합입니다. X의 두 수준에 동일한 수의 관측값이 있으면 S 값은 값 순서화 시 X의 마지막 수준에 대응합니다.
Z
Z 값은 다음과 같이 정의됩니다.
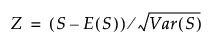
참고: Wilcoxon 검정에서는 연속성 수정이 추가됩니다. (S - E(S))가 0보다 크면 분자에서 0.5를 뺍니다. (S - E(S))가 0보다 작으면 분자에 0.5를 더합니다.
E(S)
귀무가설하의 S 기대값입니다. 더 작은 수준 또는 값 순서화 시 마지막 수준(두 그룹의 관측값 수가 동일한 경우)의 관측값 수는 nl로 나타냅니다.
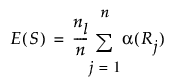
Var(S)
모든 관측값의 평균 스코어를 ave라고 정의할 경우 S의 분산은 다음과 같이 정의됩니다.
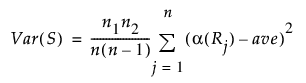
Friedman 순위 검정의 2표본 정규 근사
Friedman 순위 검정을 사용하는 경우 2표본 정규 근사에 대한 계산은 위와 동일하되 S의 분산만 다릅니다. S의 분산은 다음과 같이 계산됩니다.
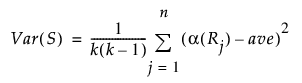
일원 카이제곱 근사
참고: Wilcoxon 스코어를 기반으로 하는 카이제곱 검정은 Kruskal-Wallis 검정이라고 합니다.
이 섹션에서 사용되는 표기는 표기에 정의되어 있습니다. 카이제곱 통계량을 계산하는 데는 다음과 같은 통계량이 사용됩니다.
Ti
X의 i번째 수준에 대한 총 스코어입니다.
E(Ti)
수준 간에 차이가 없다는 귀무가설하에 수준 i의 총 스코어에 대한 기대값으로, 다음과 같이 정의됩니다.
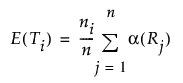
Var(T)
모든 관측값의 평균 스코어를 ave라고 정의할 경우 T의 분산은 다음과 같이 정의됩니다.
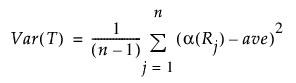
이 검정 통계량의 값은 아래와 같이 구합니다. 이 통계량은 자유도가 k – 1인 점근적 카이제곱 분포를 따릅니다.
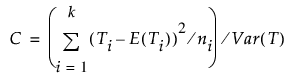
Friedman 순위 검정에 대한 일원 카이제곱 근사
Friedman 순위 검정에 대한 카이제곱 검정 통계량은 다음과 같이 계산됩니다.