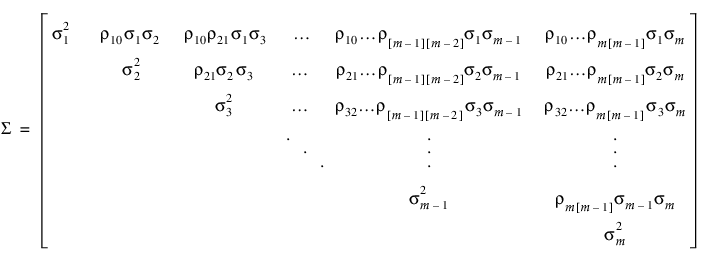반복 공분산 구조에 대한 통계 상세 정보
이 섹션에서는 모형 적합 플랫폼의 혼합 모형 분석법에서 다음 공분산 구조에 대한 파라미터화를 제공합니다.
이분산 공분산 구조
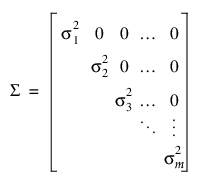
시간 j에서 관측값 간의 분산은 다음과 같습니다.
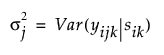
분산은 반복 열의 수준마다 다를 수 있습니다. 서로 다른 수준에서 관측값 간의 공분산은 0입니다.
비정형 공분산 구조
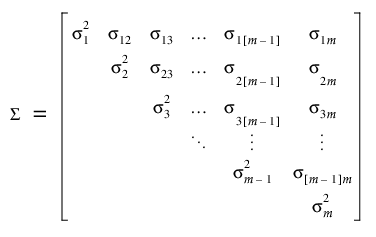
시간 j에서 관측값 간의 분산은 다음과 같습니다.
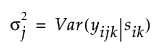
시간 j및 j¢에서 관측값 간의 공분산은 다음과 같습니다.
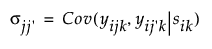
분산은 반복 열의 수준마다 다를 수 있습니다. 서로 다른 수준에서 관측값 간의 공분산은 고유합니다.
복합 대칭 공분산 구조
JMP에서 복합 대칭 공분산 구조는 독립 오차 방법의 혼합 모형을 사용하여 구현됩니다. 임의 효과는 두 가지 범주(G측 또는 R측)로 분류됩니다. 자세한 내용은 Searle et al. 연구 자료(1992)에서 확인하십시오.
G측 임의 효과는 임의 효과에 대한 설계 행렬과 관련됩니다. R측 임의 효과는 잔차 오차와 관련됩니다. 개체 내 분산은 설계 구조의 일부이며 G측에서 모델링됩니다. 개체 간 분산은 잔차 구조에 속하며 R측에서 모델링됩니다. 독립 구조의 분산은 다음과 같은 방식으로 모델링됩니다.
• 임의 효과 G측 분산은 sik ~ iid N(0, ss2)으로 모델링됩니다.
• R측 분산은 eijk ~ iid N(0, s2)으로 모델링됩니다.
그러면 공분산 행렬이 다음과 같이 정의됩니다.
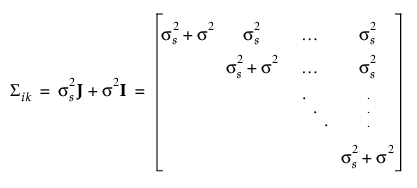
여기서 J는 1로 구성된 행렬이고 I는 항등 행렬입니다.
모든 분산을 R측에서 모델링할 수도 있습니다. 가우시안 가정을 고려할 때 이 복합 대칭 공분산 구조는 독립 모형(SAS의 Type=CS)과 동일합니다. 이 구조는 JMP에서 반복 구조 탭의 복합 대칭 구조를 통해 사용할 수 있습니다. 여기서 반복 관측값 쌍 간의 상관관계는 관측값 간의 시간 차이에 관계없이 동일합니다. 따라서 상관 행렬을 다음과 같이 지정할 수 있습니다.
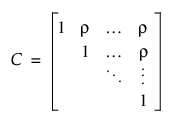
또한 JMP에서 복합 대칭 구조를 사용하면 모든 시점에서 관측값 간에 공통 분산(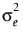
)을 가정할 수 있습니다. 그러면 공분산 구조는 
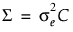이고, 다음과 같습니다.
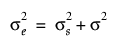
및
.
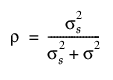여기서 r은 급내 상관계수이고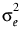 
은 잔차 분산입니다. JMP에서 복합 대칭 이분산 구조를 사용할 수도 있습니다. 이 방법은 시점에 따라 분산이 다를 수 있습니다. 그러면 다음과 같은 공분산 행렬이 생성됩니다.
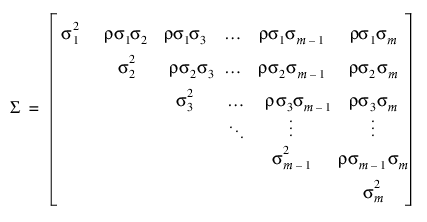
AR(1) 공분산 구조
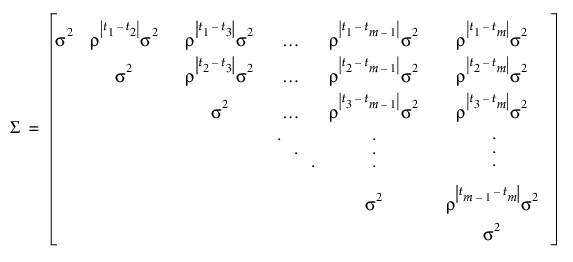
여기서 tj는 관측값 j의 시간입니다. 이 구조에서 지정된 시간의 관측값은 동일한 분산(s2)을 가집니다. r(-1 < r < 1) 모수는 한 단위 시간 간격을 갖는 두 관측값 간의 상관입니다. 관측값 간의 시간 차이가 증가하면 r 모수가 더 크게 거듭제곱되므로 공분산이 감소합니다. 대부분 AR(1)은 제1종 오류 제어를 유지하면서 더 높은 검정력으로 개체 내 상관을 위한 적절한 모형을 제공합니다.
Toeplitz 공분산 구조
Toeplitz 구조에서 고정된 수의 시간 단위로 구분된 관측값은 동일한 상관을 가집니다. AR(1) 상관 구조와 달리 고정된 시간 차이에서 Toeplitz 상관은 임의적입니다. d 단위 간격의 관측값에 대한 상관을 rd로 나타냅니다. 상관 행렬은 다음과 같이 정의됩니다.
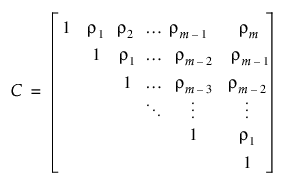
JMP의 다음 두 옵션은 이 상관 행렬을 사용합니다.
• Toeplitz 구조는 모든 시점의 관측값에 대해 공통 분산(s2)을 가정합니다. 공분산 구조는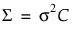 
입니다.
• Toeplitz 이분산 구조를 사용하면 시점에 따라 분산이 다를 수 있습니다.
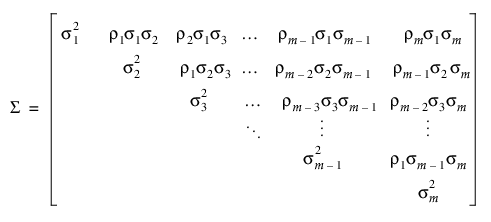
Antedependent 공분산 구조
Antedependence 모형은 유연하고 시간에 따라 상관 구조가 달라질 수 있는 일반 모형입니다. 이 모형에서 인접한 시점 j - 1과 j에서 두 관측값 간의 상관은 고유하며 rj[j−1]로 나타냅니다.
인접하지 않은 시점 j와j¢에서 관측값 쌍 간의 상관은 그 사이에 있는 모든 인접 상관의 곱입니다.
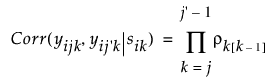
예를 들어 시점 j=2와 j¢=6에서 관측값 쌍 간의 상관은 r21r32r43r54가 됩니다.
상관 행렬은 다음과 같이 정의됩니다.
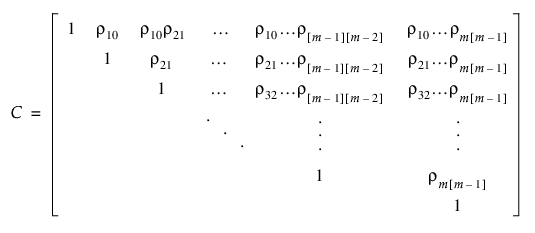
JMP의 다음 두 옵션은 이 상관 행렬을 사용합니다.
• Antedependent 등분산 구조는 상관이 달라질 수 있다는 것은 허용하지만 전체 관측 시간에서 동일한 분산을 가정합니다. 관측값 간의 분산은 항상 s2이고 공분산 행렬은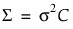 
입니다.
• Antedependent 구조를 사용하면 지정된 시간에서 관측값 간의 분산이 달라질 수 있습니다. 시간 j에서 관측값 간의 분산은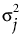 
로 나타냅니다. 그러면 공분산 행렬이 다음과 같이 정의됩니다.
