요약 통계량에 대한 통계 상세 정보

이 섹션에는 "분포 요약 통계량" 보고서의 특정 통계량에 대한 통계 상세 정보가 포함되어 있습니다. 평균, 분산, 왜도 및 첨도는 데이터를 설명하는 확률 분포의 처음 네 개 적률과 관련이 있습니다. 적률은 함수 형상에 대한 양적 측도입니다.

평균

평균은 비결측값의 합을 비결측값의 개수로 나눈 값입니다. 가중치 또는 빈도 변수를 할당한 경우 평균은 다음과 같이 계산됩니다.

1. 각 열 값에 해당 가중치 또는 빈도를 곱합니다.

2. 결과 값을 모두 더한 후 가중치 또는 빈도의 합으로 나눕니다.

표준편차

표준편차는 평균을 중심으로 한 분포의 퍼짐 정도를 측정한 것입니다. 종종 s로 표시하며, 표본 분산(s2으로 표시)의 제곱근과 같습니다.

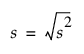
다음은 각 요소에 대한 설명입니다.

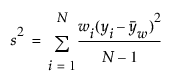
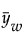= 가중 평균

평균 표준 오차

평균 표준 오차는 표본 표준편차 s를 N의 제곱근으로 나눠서 계산됩니다. 시작 창에서 가중치 또는 빈도 열을 지정한 경우에는 가중치 또는 빈도 합의 제곱근이 분모가 됩니다.

왜도

왜도는 평균에 대한 3차 적률을 기준으로 하며 다음과 같이 계산됩니다.

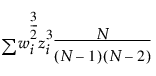여기서,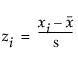

또한 wi는 가중치 항(균일 가중 항목의 경우 1)입니다.

첨도

첨도는 평균에 대한 3차 적률을 기준으로 하며 다음과 같이 계산됩니다.

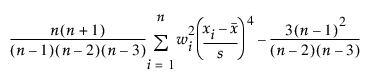
여기서 wi는 가중치 항(균일 가중 항목의 경우 1)입니다. 이 계산식을 사용할 경우 정규 분포의 첨도는 0입니다. 이 계산식을 종종 초과 첨도라고 합니다.

더 많은 정보를 원하십니까? 질문이 있습니까? JMP 사용자 커뮤니티에서 답변 받기 (community.jmp.com).