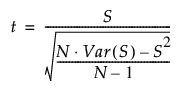Wilcoxon 부호 순위 검정에 대한 통계 상세 정보
분포 플랫폼에서 Wilcoxon 부호 순위 검정을 사용하여 단일 모집단의 중앙값을 검정하거나 일반적인 중앙값의 매칭 쌍 데이터를 검정할 수 있습니다. 매칭 쌍의 경우에는 검정 범위를 줄여 중앙값 0에 대한 쌍체 차이로 구성된 단일 모집단을 검정합니다. 검정 시 기본 모집단은 대칭적인 것으로 가정됩니다.
Wilcoxon 검정에서는 동일 값이 허용됩니다. 차이가 0인 경우에는 Pratt이 제안한 방법을 사용하여 검정 통계량이 조정됩니다. 자세한 내용은 Lehmann and D’Abrera 연구 자료(2006), Pratt 연구 자료(1959) 및 Cureton 연구 자료(1967)에서 확인하십시오.
단일 모집단의 중앙값 검정
• 다음과 같이 N개의 관측값이 있습니다.
X1, X2,..., XN
• 귀무가설은 다음과 같습니다.
H0: X의 분포가 m을 기준으로 대칭적입니다.
• 관측값과 가설 값 m 사이의 차이는 다음과 같이 계산됩니다.
Dj = Xj - m
매칭 쌍 데이터를 사용하여 두 모집단 중앙값의 동일 여부 검정
매칭 쌍 데이터에는 특수한 형태의 Wilcoxon 부호 순위 검정이 적용됩니다.
• 다음과 같이 두 개의 모집단에서 얻은 N쌍의 관측값이 있습니다.
X1, X2,..., XN 및 Y1, Y2,..., YN
• 귀무가설은 다음과 같습니다.
H0: X - Y의 분포가 0을 기준으로 대칭적입니다.
• 관측값 쌍 사이의 차이는 다음과 같이 계산됩니다.
Dj = Xj -Yj
Wilcoxon 부호 순위 검정 통계량
이 검정 통계량은 부호 순위의 합을 기준으로 합니다. 부호 순위는 다음과 같이 정의됩니다.
• 차이 절대값 ÷Dj÷는 작은 값부터 큰 값의 순서로 순위화됩니다.
• 차이가 0인 경우가 있더라도 순위는 값 1부터 시작합니다.
• 동일한 절대 차이가 있는 경우에는 해당 관측값 순위의 평균 또는 중간 순위가 할당됩니다.
차이 Dj의 순위 또는 중간 순위는 Rj로 나타냅니다. Dj의 부호 순위는 다음과 같이 정의합니다.
• 차이 Dj가 양수이면 부호 순위는 Rj입니다.
• 차이 Dj가 0이면 부호 순위는 0입니다.
• 차이 Dj가 음수이면 부호 순위는 -Rj입니다.
부호 순위 통계량은 다음과 같이 계산됩니다.
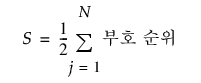
다음을 정의합니다.
d0 - 0과 동일한 부호 순위의 개수입니다.
R+ - 양수 부호 순위의 합입니다.
그런 후 다음을 구합니다.
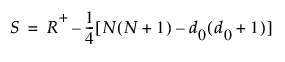
Wilcoxon 부호 순위 검정 p 값
N ≤ 20인 경우 정확 p 값이 계산됩니다.
N > 20인 경우 아래에 정의된 것과 같이 이 통계량에 대한 스튜던트 t 근사가 사용됩니다. 이때 동일 값에 대해서는 수정이 적용됩니다. 자세한 내용은 Iman 연구 자료(1974) 및 Lehmann and D’Abrera 연구 자료(2006)에서 확인하십시오.
귀무가설하에서 S의 평균은 0입니다. S의 분산은 다음과 같이 구합니다.
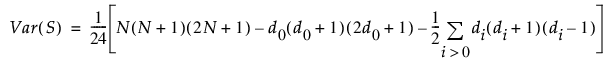
Var(S) 표현식의 마지막 합은 동일 값을 수정한 것입니다. i > 0인 경우에 대한 표기인 di는 0이 아닌 부호 순위의 i번째 그룹에 있는 값의 개수를 나타냅니다. 특정 부호 순위에 대해 동일 값이 없으면 di = 1이고 합은 0입니다.
다음 계산식으로 구한 통계량 t는 자유도가 N - 1인 근사 t 분포를 갖습니다.