공차 구간에 대한 통계 상세 정보
이 섹션에는 분포 플랫폼의 단측 및 양측 공차 구간에 대한 통계 상세 정보가 포함되어 있습니다.
정규 분포 기반의 구간
단측 구간
단측 구간은 다음과 같이 계산됩니다.
하한 =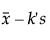 
상한 =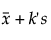 
다음은 각 요소에 대한 설명입니다.
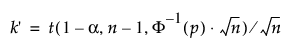
s - 표준편차입니다.
t - 비중심 t 분포의 분위수입니다.
F-1 - 표준 정규 분위수입니다.
양측 구간
양측 구간은 다음과 같이 계산됩니다.
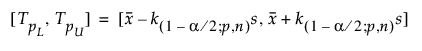
여기서 s는 표준편차이고 k(1-a/2; p,n)는 상수입니다.
k를 확인하려면 공차 구간으로 구한 모집단의 비율을 고려합니다. Tamhane and Dunlop 연구 자료(2000)에서는 이 비율을 다음과 같이 정의합니다.
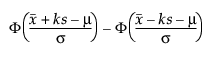
여기서 F는 표준 정규 CDF(누적 분포 함수)입니다.
따라서 k는 다음 방정식의 해를 구합니다.
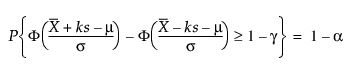
여기서 1 - g는 공차 구간에 포함된 모든 미래 관측값의 비율입니다.
정규 분포 기반 공차 구간에 대한 자세한 내용은 Meeker et al. (2017)의 표 J.1a, J.1b, J.6a 및 J.6b에서 확인하십시오.
비모수 구간
단측 하한
크기가 n인 표본에서 표집된 분포의 최소 비율 b를 포함하기 위한 100(1 - a)% 단측 공차 하한은 순서 통계량 x(l)입니다. 지수 l은 다음과 같이 계산됩니다.
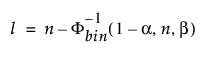
여기서 F-1bin(1-a, n, b)는 시행 횟수가 n이고 성공 확률이 b인 이항 분포의 (1 - a)번째 분위수입니다.
실제 신뢰 수준은 Fbin(n-l, n, b)로 계산되며, 여기서 Fbin(x, n, b)는 시행 횟수가 n이고 성공 확률이 b인 이항 분포 확률 변수가 x보다 작거나 같을 확률입니다.
단측 분포 무관 공차 하한을 계산하려면 표본 크기 n이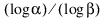 
이상이어야 합니다.
단측 상한
크기가 n인 표본에서 표집된 분포의 최소 비율 b를 포함하기 위한 100(1 - a)% 단측 공차 상한은 순서 통계량 x(u)입니다. 지수 u는 다음과 같이 계산됩니다.
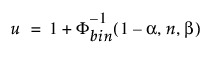
여기서 F-1bin(1-a, n, b)는 시행 횟수가 n이고 성공 확률이 b인 이항 분포의 (1 - a)번째 분위수입니다.
실제 신뢰 수준은 Fbin(u-1, n, b)로 계산되며, 여기서 Fbin(x, n, b)는 시행 횟수가 n이고 성공 확률이 b 인 이항 분포 확률 변수가 x보다 작거나 같을 확률입니다.
단측 분포 무관 공차 상한을 계산하려면 표본 크기 n이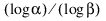 
이상이어야 합니다.
양측 구간
크기가 n인 표본에서 비율 b 이상의 표본 분포를 포함하기 위한 100(1 - a)% 양측 공차 구간은 다음과 같이 계산됩니다.
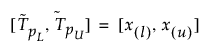
여기서 x(i)는 i번째 순서 통계량이며, l 및 u는 다음과 같이 계산됩니다.
n = n - F-1bin(1-a, n, b)라고 가정합니다. 여기서 F-1bin(1-a, n, b)는 시행 횟수가 n이고 성공 확률이 b인 이항 분포의 (1 - a)번째 분위수입니다. n가 2보다 작으면 양측 분포 무관 공차 구간을 계산할 수 없습니다. n가 2보다 크거나 같으면 l = floor(n/2)이고 u = floor(n + 1 - n/2)입니다.
실제 신뢰 수준은 Fbin(u-l-1, n, b)로 계산되며, 여기서 Fbin(x, n, b)는 시행 횟수가 n이고 성공 확률이 b 인 이항 분포 확률 변수가 x보다 작거나 같을 확률입니다.
양측 분포 무관 공차 구간을 계산하려면 표본 크기 n이 다음 방정식의 n 이상이어야 합니다.
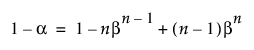
분포 무관 공차 구간에 대한 자세한 내용은 Meeker et al. 연구 자료(2017, sec. 5.3)에서 확인하십시오.