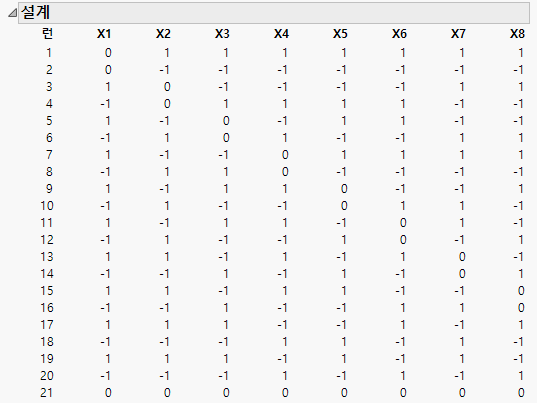
확증적 선별 설계의 구조
Figure 8.21에서는 8개의 연속형 요인과 가짜 요인에 해당하는 4개의 추가 런을 사용한 확증적 선별 설계의 예를 보여 줍니다. 다음 사항에 유의하십시오.
• 각 행 쌍은 접기 쌍이며 짝수 번호 행의 값은 이전 행의 -1배입니다. 설계 접기를 수행하면 2요인 교호작용과 주효과의 교락이 제거됩니다.
• 각 요인은 3회 런의 중앙값으로 설정되며 설계 구성과 함께 모든 2차 효과를 추정할 수 있게 합니다.
• 17 ~ 20 행은 가짜 요인에 해당하는 추가 런입니다.
• 마지막 행에 중앙점 런을 추가하면 절편 및 모든 주효과와 2차 효과를 포함하는 모형을 적합시킬 수 있습니다.
이 구조는 연속형 요인에 대한 확증적 선별 설계의 대표적인 예입니다.
그림 8.21 8개의 연속형 요인에 대한 확증적 선별 설계
컨퍼런스 행렬 및 런 수
JMP의 확증적 선별 설계는 컨퍼런스 행렬(Xiao et al., 2012)을 사용하여 구성됩니다. 컨퍼런스 행렬은 m x m 행렬 C입니다. 여기서 m은 짝수입니다. C 행렬은 대각 항목이 0, 비대각 항목이 1 또는 –1이고 다음을 충족합니다.
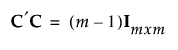 .
.
참고: m의 특정 짝수 값에 대해 컨퍼런스 행렬이 있는지 여부는 알 수 없습니다.
요인 수 k가 5 이상이라고 가정해 보겠습니다. k ≤ 4 요인인 경우에는 4개 이하의 요인에 대한 확증적 선별 설계의 설명을 참조하십시오.
k개의 연속형 요인의 경우 컨퍼런스 행렬을 사용할 수 있다고 가정해 보겠습니다.
• k가 짝수인 경우 k x k 컨퍼런스 행렬을 사용하여 설계의 k회 런을 정의합니다. 음의 –C는 설계 접기한 런을 정의합니다. 절편, 주효과 및 2차 효과를 포함하는 모형을 추정할 있도록 설계에 중앙점이 추가됩니다. 따라서 짝수 k에 대해 확증적 선별 설계의 최소 런 수는 2k + 1입니다.
• k가 홀수인 경우 (k+1) x (k+1) 컨퍼런스 행렬이 사용되고 마지막 열은 삭제됩니다. 중앙점이 추가됩니다. 따라서 홀수 k에 대해 선별 설계의 최소 런 수는 2k + 3입니다.
일부 요인이 범주형이고 컨퍼런스 행렬을 사용할 수 있는 경우 비슷한 프로시저가 사용됩니다. 자세한 내용은 Jones and Nachtsheim(2013)에서 확인하십시오.
• 단일 중앙점 대신 두 개의 추가 런이 필요합니다. 이 두 런은 모든 연속형 요인이 중간 값으로 설정된 중앙점 런입니다.
• k개 요인이 있고 k가 짝수인 경우 설계의 런 수는 2k + 2입니다.
• k가 홀수인 경우 런 수는 2k + 4입니다.
컨퍼런스 행렬을 사용할 수 없는 m 값에 대해서는 그 다음으로 큰 컨퍼런스 행렬을 사용하여 확증적 선별 설계를 구성할 수 있습니다. 결과적으로 필요한 런 수는 연속형 요인의 경우 2k + 3, 범주형 요인의 경우 2k + 4를 초과할 수 있습니다.
추가 런
추가 런은 가상(가짜) 요인을 사용하여 구성됩니다. f개의 가짜 요인을 설계에 추가하면 2f개의 추가 런이 생깁니다.
실험 연구에서 요인 수는 k로 나타냅니다. 4개 또는 8개의 추가 런을 설계에 추가할 수 있습니다. 추가 런은 컨퍼런스 행렬 및 런 수에서 설명된 것처럼 k + f개의 요인에 대한 설계를 생성한 후 마지막 f 개 열을 삭제하여 구성합니다. 추가 런이 4개만 있어도 모형 선택에 매우 유용할 수 있습니다.
추가 런을 사용하는 방법에 대한 자세한 내용은 DSD를 위한 유효 모형 선택에서 확인하십시오.
4개 이하의 요인에 대한 확증적 선별 설계
4개 이하의 요인에 대한 확증적 선별 설계는 5개 요인의 확증적 선별 설계를 기준으로 사용하여 구성됩니다. 컨퍼런스 행렬 방법에 따라 엄격하게 구성된 k ≤ 4 요인 설계의 경우 바람직하지 않은 특성이 있기 때문입니다. 특히 2차 효과(second-order effect)를 분리하기가 어렵습니다.
k ≤ 4 요인을 지정하면 5개 요인에 대한 확증적 선별 설계가 구성되고 불필요한 열이 삭제됩니다. 따라서 k ≤ 4 요인이 포함된 블록화되지 않은 설계의 런 수는 모든 요인이 연속형인 경우 13이고 일부 요인이 범주형인 경우에는 14입니다.