확증적 선별 설계

DSD(확증적 선별 설계)는 선별 설계입니다. 이 설계는 일반적으로 4개 이상의 요인이 있는 초기 단계 실험 작업에 적합합니다. DSD는 연속형 요인 또는 2수준 범주형 요인의 조합에 사용될 수 있습니다. 대부분의 요인이 연속형일 때 가장 잘 작동합니다. 각 연속형 요인은 연속형 요인에 대한 2차 모형 항을 조사할 수 있는 세 가지 수준을 사용합니다.

다음과 같은 면에서 확증적 선별 설계가 표준 선별 설계보다 우수하다고 할 수 있습니다.

• 각 연속형 요인을 세 가지 수준으로 처리하여 비선형 효과의 원인을 식별하는 데 도움이 됩니다. 표준 선별 설계의 연속형 요인에는 두 가지 수준만 있습니다. 선별 설계에 중앙점을 추가할 수 있지만 이 점은 곡률이 있는 경우에만 설정됩니다. 2차 효과의 원인이 되는 요인은 식별할 수 없습니다.

• 2차까지의 모든 효과 사이에 교락을 방지합니다. 연속형 요인을 사용하는 확증적 선별 설계의 주효과는 다른 주효과와 서로 직교하고 2요인 교호작용 및 2차 효과와 직교합니다. 2요인 교호작용은 서로 완전히 교락되지 않습니다. 런 수가 비슷한 많은 표준 선별 설계에서는 교락이 발생합니다.

• 표준 선별 설계의 초기 결과에서 모호성을 해결하기 위해 비용이 많이 드는 추가 실험이 필요하지 않습니다.

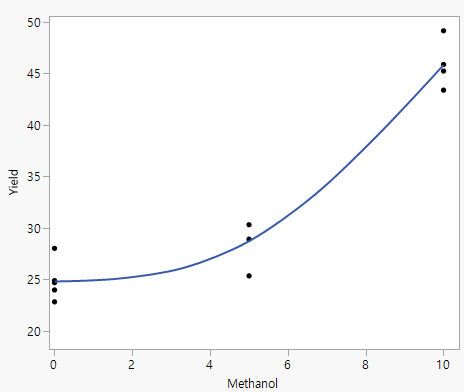
그림 8.1 곡률을 보여 주는 요인 값 대 반응 그림 

목차

확증적 선별 설계 개요

확증적 선별 설계의 예

확증적 선별 설계 생성

반응

요인

설계 옵션

설계

설계 평가

출력 옵션

확증적 선별 설계 옵션

반응 시뮬레이션

확증적 선별 설계의 추가 예

확증적 선별 설계와 부분 요인 설계의 비교 예

블록화를 사용한 확증적 선별 설계의 예

확증적 선별 설계와 Plackett-Burman 설계의 비교 예

확증적 선별 설계에 대한 통계 상세 정보

확증적 선별 설계의 구조

실험 데이터 분석

더 많은 정보를 원하십니까? 질문이 있습니까? JMP 사용자 커뮤니티에서 답변 받기 (community.jmp.com).