두 개의 기본 적합 기계

통계적 적합에 대한 놀라운 사실은 대부분의 전통적 설계 방법이 스프링과 압력 실린더라는 두 가지 간단한 기계를 사용하는 것으로 축소된다는 것입니다.

스프링

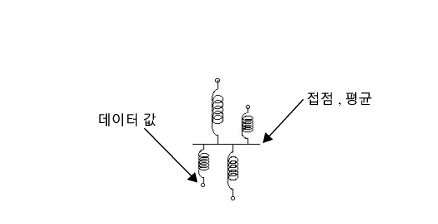
먼저, 스프링은 연속형 반응 모형에 대한 적합 기계입니다(Farebrother 1987). n개의 점이 있고 점의 기대값(평균)을 알고 싶다고 가정해 보겠습니다. 점을 배치한 후 스프링으로 공통 접합부에 점을 연결하면 어떻게 될지 예상해 봅니다(Figure A.7). 손을 놓으면 스프링이 접점을 위아래로 움직이다가 중간 지점에서 멈춥니다. 이것은 물리학에 의해 발생하는 현상입니다.

스프링이 부착된 접점을 평균으로 데이터가 정규 분포를 따르는 경우 각 점의 스프링에서 발생하는 물리적 에너지는 데이터 점의 불확도에 비례합니다. 스프링의 에너지, 즉 불확도를 계산하려면 각 점에서 평균까지의 거리에 대한 제곱합을 계산해야 합니다.

관측된 데이터에 대한 불확도를 최소화하는 추정값을 선택하기 위해 스프링 안정점이 평균 추정값으로 선택됩니다. 이 점은 스프링을 늘리기 위해 최소 에너지가 필요한 지점이며 최소 제곱 적합과 동등합니다.

그림 A.7 데이터 점에 스프링 연결 

이 방법으로 하나 이상의 평균을 적합시킵니다. 또한 선, 평면 또는 초평면을 적합시킵니다. 이 방법은 연속형 데이터에 대한 거의 모든 모형을 적합시킬 수 있습니다. 스프링을 늘려야 하는 거리의 제곱합으로 에너지 또는 불확도를 측정합니다.

통계학자들은 최소한의 신뢰를 요구하는 정규 분포를 믿습니다. 어떤 의미에서는 가장 랜덤하다고 할 수 있습니다. 분포에 대한 가장 무정보적인 모양을 갖고 있습니다. 즉, 주어진 분산에 대해 예상되는 불확도가 가장 높은 분포입니다. 이 분포의 불확도는 제곱 거리로 측정됩니다. 대부분의 경우 분포가 혼합되어 있거나 독립 통계량의 합이 있을 때 이 분포가 극한 분포입니다. 이 분포를 사용하면 검정 통계량을 상당히 쉽게 측정할 수 있습니다.

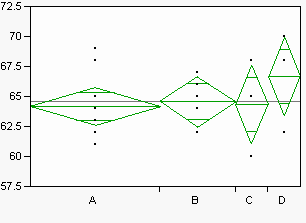
가설에 의해 적합이 제약되는 경우 동일한 스프링 에너지를 측정하여 가설을 검정합니다. 실험에서 네 가지 서로 다른 처리의 반응이 있고 평균이 유의하게 다른지 검정하려는 경우를 가정해 보겠습니다. 먼저 Figure A.8에 나오는 것처럼 데이터가 그룹으로 표시되었지만 각 처리에 대한 개별 평균에 스프링이 연결되어 있다고 생각해 봅니다. 그런 다음 스프링력에 압력을 가하여 개별 평균을 공통 평균으로 이동합니다. 결과는 어떻게 될까요? 평균이 같아지도록 누르는 에너지의 양이 바로 필요한 검정 통계량입니다. 해당 에너지는 평균이 같은지 여부를 검정하는 가설에 대한 F-검정의 주요 성분입니다.

그림 A.8 연속형 반응 변수에 대한 일원 그림 

압력 실린더

반응이 연속형 대신 범주형이면 어떻게 될까요? 예를 들어 반응이 자동차 표본의 생산 국가인 경우를 가정해 보겠습니다. 표본에 대해 American, European, Japanese라는 세 가지 반응 수준의 확률이 있습니다. 생산 국가에 대한 이러한 확률을 몇 가지 추정값으로 설정한 후 데이터의 불확도를 평가할 수 있습니다. 이 불확도는 데이터에 의해 제공된 반응 확률의 음의 로그를 합산하여 구합니다. 이 행렬은 다음과 같이 정의됩니다.

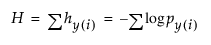
스프링 개념은 평균이 연속형 데이터에 어떻게 적합되는지 보여 줍니다. 반응이 범주형인 경우 통계 방법은 반응 확률을 직접 추정하고 데이터의 전체 불확도를 최소화하는 추정값을 선택합니다. 확률 추정값은 음수가 아니고 합이 1이어야 합니다. 반응 확률을 총 길이가 1인 척도의 구성 요소로 생각할 수 있습니다. 각 반응 관측값의 경우, 타이어 펌프와 같은 가스 압력 실린더를 반응 영역에 넣습니다. 최저 위치 에너지의 평형에 도달할 때까지 반응 수준 간의 파티션을 다르게 변경합니다. 그러면 결과 파티션의 크기를 사용하여 반응 확률이 추정됩니다.

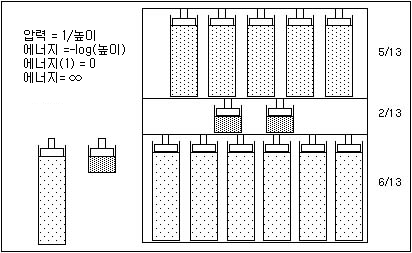
Figure A.9에서는 medium 크기 자동차와 같은 단일 범주의 상황을 보여 줍니다. Figure A.10에서 medium 라벨이 지정된 Carpoll.jmp의 모자이크 열을 참조하십시오. 13개의 반응(자동차)이 있다고 가정합니다. 첫 번째 수준(American)의 반응은 6개이고 다음 수준과 마지막 수준의 반응은 각각 2개, 5개입니다. 총 에너지를 최소화하도록 반응 파티션에 대한 압력이 균형을 이루기 때문에 반응 확률은 각각 6/13, 2/13, 5/13가 됩니다.

그림 A.9 파티션에서 압력 실린더의 효과 

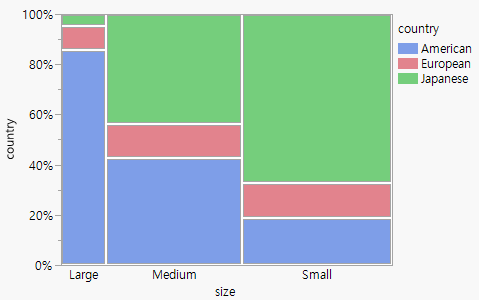
연속형 데이터에 대한 스프링과 마찬가지로 일부 요인에 따라 표본을 나누고 개별 파티션 집합을 적합시킬 수 있습니다. 그런 다음 파티션을 동일하게 만드는 데 필요한 추가 에너지 양을 측정하여 반응률이 그룹 전체에서 같은지 검정합니다. 자동차 크기별로 그룹화된 자동차 생산 국가 확률에 대한 압력 실린더를 상상해 봅니다. 각 그룹의 파티션을 수평으로 정렬하는 데 필요한 에너지로 변수의 확률이 같은지 여부를 검정합니다. Figure A.10에서는 이러한 파티션을 보여 줍니다.

그림 A.10 범주형 데이터에 대한 모자이크 그림