Power Analysis

Power is the probability of detecting an active effect of a given size. The Power Analysis report helps you evaluate and compare the ability of your designs to detect effects of practical importance. For each of your designs, the Power Analysis report calculates the power of tests for the effects in the Model outline.

The Power Analysis report gives the power of tests for individual model parameters and for whole effects. It also provides a Power Plot and a Power versus Sample Size plot.

Power depends on the number of runs, the significance level, and the estimated error variation. For more information about how power is calculated, see Power Calculations.

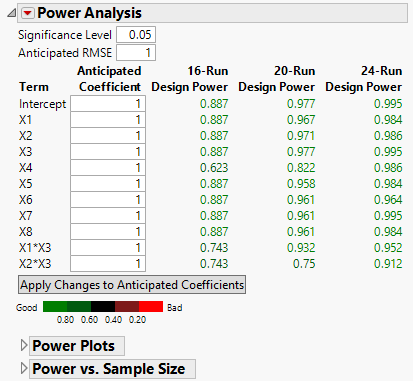
Figure 16.20 Power Analysis Outline for Three Designs 

Figure 16.20 shows the Power Analysis outline for the three designs constructed in Designs of Different Run Sizes. Two two-way interactions have been added to the Model outline.

Power Analysis Report

When you specify values for the Significance Level and Anticipated RMSE, they are used to calculate the power of the tests for the model parameters. Enter coefficient values that reflect differences that you want to detect as Anticipated Coefficients. To update the results for all designs, click Apply Changes to Anticipated Coefficients.

Significance Level

The probability of rejecting the hypothesis of no effect, if it is true. The power calculations update immediately when you enter a value.

Anticipated RMSE

An estimate of the square root of the error variation. The power calculations update immediately when you enter a value.

The power values are colored according to a color gradient that appears under the Apply Changes to Anticipated Coefficients button. You can control the color legend using the options in the Power Analysis red triangle menu. See Color Dashboard.

For more information about the Power Plots, see Power Plot.

Note: If the design is supersaturated, meaning that the number of parameters to be estimated exceeds the number of runs, the Power Analysis outline lists only a set of effects that can be estimated.

Tests for Individual Parameters

The Term column contains a list of model terms. For each term, the Anticipated Coefficient column contains a value for that term. The Power value is the power of a test that the coefficient for the term is zero if the true value of the coefficient is given by the Anticipated Coefficient, given the design, and the terms in the Model outline.

Term

The model term associated with the coefficient being tested.

Anticipated Coefficient

A value for the coefficient associated with the model term. This value is used in the calculations for Power. When you set a new value in the Anticipated Coefficient column, click Apply Changes to Anticipated Coefficients to update the Power calculations.

Note: The anticipated coefficients have default values of 1 for continuous effects. They have alternating values of 1 and –1 for categorical effects.

Power

The probability of rejecting the null hypothesis of no effect when the true coefficient value is given by the specified Anticipated Coefficient.

– For a coefficient associated with a numeric factor, the change in the mean response from the high to low setting (based on the model) is twice the coefficient value.

– For a coefficient associated with a categorical factor, the change in the mean response (based on the model) across the levels of the factor equals twice the absolute value of the anticipated coefficient. For more information on power for categorical factors, see Tests for Categorical Effects with More Than Two Levels

Calculations use the specified Significance Level and Anticipated RMSE. For more information about the power calculation, see Power for a Single Parameter.

Apply Changes to Anticipated Coefficients

When you set a new value in the Anticipated Coefficient column, click Apply Changes to Anticipated Coefficients to update the Power values.

Tests for Categorical Effects with More Than Two Levels

If your model contains a categorical effect with more than two levels, then the following columns appear below the Apply Changes to Anticipated Coefficients button:

Effect

The categorical effect.

Power

The power calculation for a test of no effect. The null hypothesis for the test is that all model parameters corresponding to the effect are zero. The difference to be detected is defined by the values in the Anticipated Coefficient column that correspond to the model terms for the effect. The power calculation reflects the differences in response means determined by the anticipated coefficients.

Calculations use the specified Significance Level and Anticipated RMSE. For more information about the power calculation, see Power for a Categorical Effect.

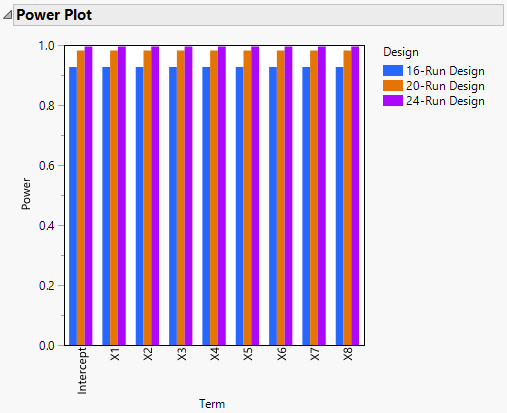
Power Plot

The Power Plot shows the power values from the Power Analysis in graphical form. The plot shows the power for each effect and for each design in a side-by-side bar chart.

Figure 16.21 Power Plot for Three Designs 

The Power Plot in Figure 16.21 is for the main effects of the three designs constructed in Designs of Different Run Sizes.

Power versus Sample Size

The Power versus Sample Size plots appears only when the designs that you are comparing differ in run size. The plots enables you to see how sample size affects power for each effect in the model. It conveys the same information as is in the Power Plots graph, but in a different format. The power values at integer sample sizes are connected with line segments.

Figure 16.22 Power versus Sample Size Profiler for Three Designs