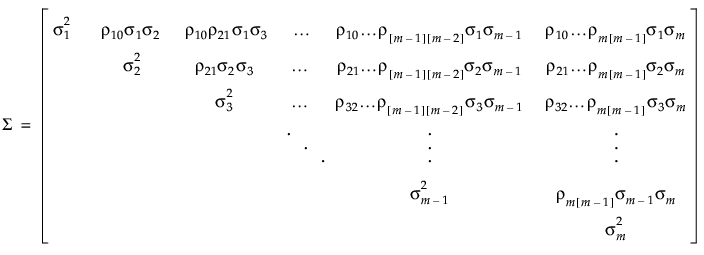この行列の対角要素は、以下のように定義される、時間jにおける誤差の分散です。
この行列の対角要素は、以下のように定義される、時間jにおける誤差の分散です。
誤差構造が複合対称(compound symmetry)である反復測定モデルは、個体を変量効果とした分割実験モデルと等価です。反復測定モデルではR行列において相関構造を表しますが、分割実験モデルでは、それと等価な構造をG行列で表します。詳細については、Searle et al.(1992)を参照してください。
|
•
|
|
•
|
ここで、tjは、第j時点の時刻です。この構造では、どの時点でも同じ分散 を持ちます。パラメータρ(‐1 < ρ < 1)は、1単位時間だけ離れた2時点の誤差間の相関です。時間の差が大きくなるにつれて、ρのべき乗が大きくなるので、誤差間の相関は小さくなります。AR(1)共分散構造は、多くの分野で個体内相関として適しており、第1種の誤りを制御しながらも、高い検出力が得られることが期待されます。
を持ちます。パラメータρ(‐1 < ρ < 1)は、1単位時間だけ離れた2時点の誤差間の相関です。時間の差が大きくなるにつれて、ρのべき乗が大きくなるので、誤差間の相関は小さくなります。AR(1)共分散構造は、多くの分野で個体内相関として適しており、第1種の誤りを制御しながらも、高い検出力が得られることが期待されます。
 を持ちます。パラメータρ(‐1 < ρ < 1)は、1単位時間だけ離れた2時点の誤差間の相関です。時間の差が大きくなるにつれて、ρのべき乗が大きくなるので、誤差間の相関は小さくなります。AR(1)共分散構造は、多くの分野で個体内相関として適しており、第1種の誤りを制御しながらも、高い検出力が得られることが期待されます。
を持ちます。パラメータρ(‐1 < ρ < 1)は、1単位時間だけ離れた2時点の誤差間の相関です。時間の差が大きくなるにつれて、ρのべき乗が大きくなるので、誤差間の相関は小さくなります。AR(1)共分散構造は、多くの分野で個体内相関として適しており、第1種の誤りを制御しながらも、高い検出力が得られることが期待されます。Toeplitz構造では、等しい時間間隔だけ離れている観測値どうしにおいて相関が同じになっています。ただし、AR(1)相関構造とは対照的に、Toeplitz構造では時間差ごとの相関は不定となっています。d単位離れた時点における誤差間の相関を とすると、 Toeplitz構造の相関行列は次のようになります。
とすると、 Toeplitz構造の相関行列は次のようになります。
 とすると、 Toeplitz構造の相関行列は次のようになります。
とすると、 Toeplitz構造の相関行列は次のようになります。|
•
|
 反復共分散構造
反復共分散構造 異分散共分散構造
異分散共分散構造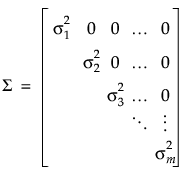
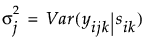
 無構造の共分散構造
無構造の共分散構造
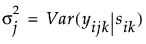
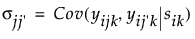
 複合対称共分散構造
複合対称共分散構造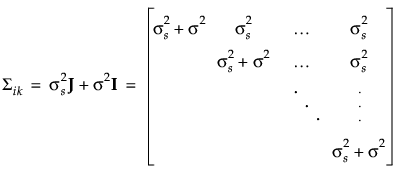
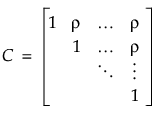
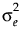 )は等しいと仮定されます。[複合対称]では、共分散構造は
)は等しいと仮定されます。[複合対称]では、共分散構造は と設定されます。この式と分割実験モデルとの関係は、
と設定されます。この式と分割実験モデルとの関係は、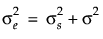
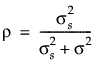 .
. は級内相関係数、
は級内相関係数、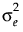 は誤差分散です。「混合モデル」手法では、単なる[複合対称]以外に、[複合対称 異分散]という構造も提供しています。[複合対称 異分散]では、時点によって誤差の分散が異なると仮定されています。
は誤差分散です。「混合モデル」手法では、単なる[複合対称]以外に、[複合対称 異分散]という構造も提供しています。[複合対称 異分散]では、時点によって誤差の分散が異なると仮定されています。
 AR(1)共分散構造
AR(1)共分散構造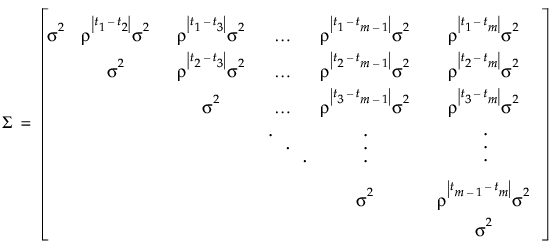
 Toeplitz 共分散構造
Toeplitz 共分散構造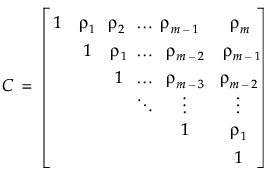
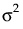 )を仮定します。共分散構造は、
)を仮定します。共分散構造は、 です。
です。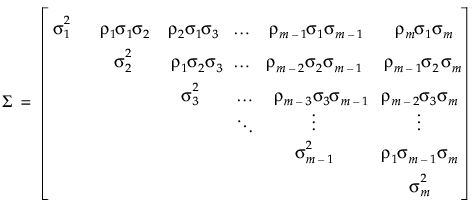
 先行依存共分散構造
先行依存共分散構造 と表されます。
と表されます。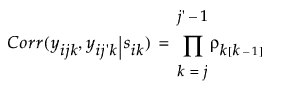
 となります。
となります。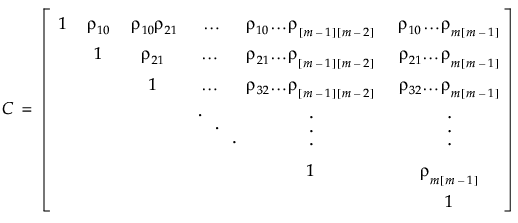
 、共分散行列は
、共分散行列は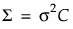 です。
です。 とします。[先行依存]構造の共分散行列は次のようになります。
とします。[先行依存]構造の共分散行列は次のようになります。