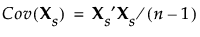このバージョンのヘルプはこれ以降更新されません。最新のヘルプは https://www.jmp.com/support/help/ja/15.2   からご覧いただけます。


多変量分析 • 主成分分析 • 「主成分分析」プラットフォームの統計的詳細 • 推定法について
前へ
 • 
次へ
推定法について
REML
データに欠測値がある場合、REML法（制限最尤法）は、最尤法に比べて、推定値のバイアスが小さいのが特徴です。REML法は、誤差対比（error contrast）から導出された周辺尤度を最大化する推定方法です。REML法は、分散および共分散を推定するのによく使われます。［多変量の相関］の［REML］は、反復測定データの相関構造に無構造（unstructured）を仮定した混合モデルのREML推定と同じです。混合モデルについては、SASシステムのPROC MIXEDに関するドキュメントを参照してください。
横長なデータに対する手法
［横長］手法では、特に列数が多くなっているデータに対して、内部計算において共分散行列を求めずに、効率的に計算を行います。このアルゴリズムは、特異値分解に基づきます。次の表記を使用します。
•
n = 行数（標本サイズ）
•
p = 変数の数
•
X = データ値のn x p行列
0以外の固有値の個数。これは求められる主成分の個数であり、Xの相関係数行列のランクと同じです。0以外の固有値の数は、nとpの小さい方を超えることはできません。
推定法として［横長］を選択した場合、データは常に標準化されます。データの標準化とは、データから平均を引き、それを標準偏差で割る変換を指します。標準化したデータを、Xs（n x p行列）と記します。標準化していないデータXの相関行列は、標準化したデータの共分散行列です。よって、次のように相関係数行列は求められます。
Xsは、特異値分解した行列によりUDiag(Λ)V’と表されます。この特異値分解により、固有ベクトルとXs’Xsの固有値が求められます。なお、主成分スコアはXsVによって求められます。詳細については、「統計的詳細」の付録「「線形 横長データ」の手法と特異値分解」（279ページ）を参照してください。
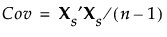
疎なデータに対する手法
［横長］手法と同様に、［疎］手法は特異値分解に基づきます。そのため、［疎］手法のアルゴリズムでは共分散行列は計算されず、効率的に計算が行われます。
第 “横長なデータに対する手法”で説明したXの同じ表記と標準化を使用すると、 Xの相関行列はXsの共分散行列によって次のように表されます。
［疎］手法は、特異値分解の計算アルゴリズムにおいて［横長］手法とは異なります。［横長］手法では完全な特異値分解を行いますが、 ［疎］手法は、特異値分解において、特異値および特異ベクトルを指定された個数しか求めません。そのため、固有値と主成分に関しても指定された個数だけしか求めません。アルゴリズムの詳細については、Baglama and Reichel（2005）を参照してください。