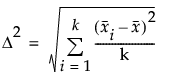ベータ分布、カイ2乗分布、F分布、ガンマ分布、正規分布、Studentのt分布、Weibull分布、TukeyのHSD検定などの統計分布の確率と分位点を求める計算式を作成できます。構文の詳細については、『スクリプト構文リファレンス』の「JSL関数」章を参照してください。
（すべての実数を定義域とする）標準正規分布の分位点を引数にとります。平均（mean）、標準偏差（std dev）の引数が指定されていない場合は、標準正規分布の密度を戻します。標準正規分布の密度曲線をグラフに描くには、まず、計算式count(-3, 3, nrow())によって、列（X）を作成します。2列目に、密度を生成する計算式Normal Density(X)を挿入します。そして、［グラフ］>［重ね合わせプロット］によって、Xに対する密度をプロットします。
（すべての実数を定義域とする）標準正規分布の分位点を引数にとります。この関数は、標準正規分布に従う確率変数がx以下になる確率を戻します。たとえば、式Normal Distribution(1.96)は0.975を戻します。これは、標準正規分布に従う確率変数が、1.96以下となる確率です。また、平均（mean）および標準偏差（std dev）の引数を指定して、標準正規分布以外の正規分布からの確率を取得することもできます。Normal Distribution関数は、Normal Quantile関数の逆関数です。
確率pを引数にとり、標準正規分布の下側累積確率がpとなる分位点を戻します。たとえば、式Normal Quantile(0.975)は標準正規分布の97.5%点である1.96を戻します。また、平均（mean）および標準偏差（std dev）の引数を指定し、標準正規分布以外の正規分布の分位点を取得することもできます。Normal Quantile関数は、Normal Distribution関数の逆関数です。
分位点と2つの形状パラメータ（αとβ）を引数として指定します。閾値パラメータ（θ）と尺度パラメータ（σ>0）も指定できます。Beta Density関数は、ベータ分布の密度関数であり、ベータ分布のxにおける密度を戻します。ベータ分布は、分位点xの定義域が無限であるような正規分布やガンマ分布とは異なり、限定された区間に対してだけ正の密度を持ちます。ベータ分布は、割合のような、範囲が0から1までに制限されている確率変数をモデル化する場合に役立ちます。
Beta Distribution関数は、2つの形状パラメータ（α>0およびβ>0）を引数にとります。閾値パラメータ（θ）と尺度パラメータ（σ）も指定できます。ここで、θ≤ x ≤θ + σです。θのデフォルト値は0です。σのデフォルト値は1です。
Beta Quantile関数は、指定された形状パラメータ（αおよびβ）を持つベータ分布の分位点関数です。ベータ分布の下側累積確率がpになる分位点xを戻します。Beta Quantile関数は、Beta Distribution関数の逆関数です。
任意の実数xと、オプションで中心（center）および尺度（scale）を引数にとります。オプションの引数が指定されていない場合、中央値が0、第3四分位数が1であるCauchy分布の、xにおける密度が戻されます。
中心と尺度の値が指定されている場合は、次のような特性を持つCauchy分布の、xにおける密度を戻します。
|
•
|
オプションの中心パラメータ（center）は、分布の中央値（メディアン）に該当します。
|
|
•
|
オプションの尺度パラメータ（scale）は、四分位範囲の半分、つまり75%の分位点と25%の分位点の差の半分に該当します。
|
任意の実数xと、オプションで中心（center）および尺度（scale）を引数にとります。オプションの引数が指定されていない場合、中央値が0、第3四分位数が1であるCauchy分布の、xにおける確率が戻されます。中心と尺度が指定されている場合は、指定された中心パラメータを中央値とし、指定された尺度を四分位範囲の半分とするCaucy分布の、xにおける下側累積確率を戻します。
引数prob（0～1における任意の値）と、オプションで中心（center）と尺度（scale）の引数をとります。オプションの引数の値が指定されていない場合、中央値が0で、第3四分位数が1であるCauchy分布の、下側累積確率がp（=prob）となる分位点を戻します。中心と尺度の値が指定されている場合は、中心が中央値、尺度の2倍が四分位範囲であるCauchy分布の、下側累積確率がpとなる分位点を戻します。
カイ2乗分布の分位点（x）、自由度（DF）、およびオプションで非心度パラメータ（centered）を引数にとります。この関数は、カイ2乗分布の累積分布関数の値を戻します。たとえば、式
ChiSquare Distribution(11.264, 5)は、非心度パラメータが0で自由度5のカイ2乗分布に従う確率変数が、11.264以下である確率を戻します。この式は0.95361を戻します。
ChiSquare Distribution(11.264, 5)は、非心度パラメータが0で自由度5のカイ2乗分布に従う確率変数が、11.264以下である確率を戻します。この式は0.95361を戻します。
ChiSquare Distribution関数は、自由度に整数でない数値も指定できます。非心度パラメータのデフォルト値は0です。ChiSquare Distribution関数は、ChiSquare Quantile関数の逆関数です。
確率（p）、自由度（DF）、および非心度パラメータ（centered）の3つを引数にとります。これは、指定された非心度パラメータと自由度のカイ2乗分布の分位点関数で、カイ2乗分布の下側累積確率がpとなる分位点を戻します。たとえば、式ChiSquare Quantile(0.95, 3.5, 4.5)は、非心度パラメータ4.5で自由度3.5のカイ2乗分布の95%点を戻します。この式は17.50458を戻します。
ChiSquare Quantile関数は、自由度に整数でない数値も指定できます。非心度パラメータのデフォルト値は0です。ChiSquare Quantile関数は、ChiSquare Distribution関数の逆関数です。
Dunnettの多重比較検定のp値を戻します。
F分布の分位点（x）、分子の自由度（DF numer）、分母の自由度（DF denom）、およびオプションで非心度パラメータ（centered）を引数にとります。この関数は、F分布の密度を戻します。
分位点（x）、分子の自由度（DF numer）、分母の自由度（DF denom）、および非心度パラメータ（centered）の4つを引数にとります。この関数は、指定された非心度パラメータと自由度のF分布で、分位点における累積分布関数の値を戻します。たとえば、式F Distribution(3.32, 2, 3)は、分子の自由度が2で分母の自由度が3のF分布に従う確率変数が3.32以下となる確率を戻します。この式は0.82639を戻します。
この関数には、自由度に整数でない数値も指定できます。デフォルトでは、非心度パラメータは0に設定されています。この関数は、F Quantile関数の逆関数です。
F分布の生存確率(上側累積確率)の対数を戻します。
F分布の下側累積確率の対数を戻します。
prob=F-Distribution (x, ndf, ddf, nc)となるような非心度パラメータncを求めます。
F Power関数は、指定された引数から、F検定またはt検定での検出力を求めます。一方、F Sample Size関数は、標本サイズを求めます。これらの関数で行われる計算は、検出力および標本サイズを、（事後的にではなく）事前に計算するときのものです。これらの関数は、［実験計画(DOE)］>［標本サイズ/検出力］と同じ計算を行います。検出力と標本サイズの詳細については、『実験計画(DOE)』の「検出力と標本サイズ」章を参照してください。これらの関数は以下の引数をとります。
|
•
|
alpha 容認できる有意水準（0.05 の場合が多い）
|
|
•
|
dfh 仮説の自由度。t検定の場合は1
|
|
•
|
|
•
|
SquaredSize 誤差分散で尺度化した効果の大きさ（effect size; 効果量）を2乗した値で、F分布の非心度パラメータを計算するために使われます。この引数には、Squared Size = Δ2/σ2（σ2は誤差分散）を指定してください。以下のように、計算をしてください。
|
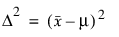1標本のt検定
2標本のt検定
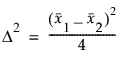k標本のF検定|
•
|
確率（p）、分子の自由度（DF numer）、分母の自由度（DF denom）、および非心度パラメータ（centered）の4つを引数にとります。これは、指定された非心度パラメータと自由度のF分布で、累積確率pに対する分位点を戻します。たとえば、式F Quantile(0.95, 2, 10, 0)は、非心度パラメータが0、分子の自由度2、分母の自由度10のF分布の95%点を戻します。この式は4.1028を戻します。
指定する引数として、ガンマ分布の分位点が必須です。オプションで、形状パラメータα>0（shape、デフォルトは1）、 尺度パラメータb>0（scale、デフォルトは1）、 および閾値パラメータ（threshold、-∞ < θ < +∞、デフォルトは0）を指定できます。
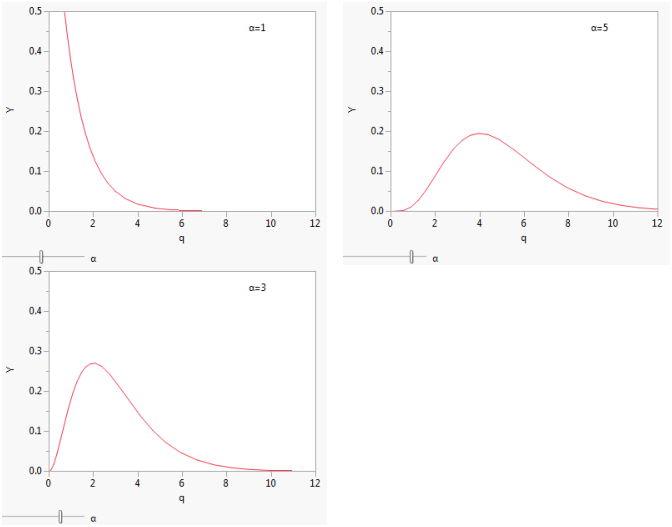
Gamma Densityの例は、形状パラメータが1、3、5のガンマ分布の密度関数の形状を示しています。標準のガンマ分布の密度関数は、α (shape) ≤1の場合、常に減少します。α > 1の場合、x = θのとき0から最大値に達するまで増加した後、減少します。
図A.12 Gamma Densityの例
分位点の値（x）を引数にとり、標準ガンマ分布の累積分布関数の値を戻します。オプションで、形状パラメータ、尺度パラメータ、閾値パラメータを指定できます。これらのデフォルト値については、前のGamma Density関数の説明を参照してください。この関数は、ガンマ分布に従う確率変数がx以下になる確率を戻します。Gamma Distribution関数は、Gamma Quantile関数の逆関数です。
確率pを引数にとり、標準ガンマ分布における下側累積確率がpとなる分位点を戻します。オプションで、形状パラメータ（shape）、尺度パラメータ（scale）、閾値パラメータ（threshold）をとります。それらのデフォルト値は、Gamma Density関数と同じです。Gamma Quantile関数は、Gamma Distribution関数の逆関数です。
パラメータがmu、sigma、およびlambdaの拡張一般化ガンマ確率分布のxにおける密度を戻します。
パラメータがmu、sigma、およびlambdaの拡張一般化ガンマ分布に基づく確率変数がxより小さい確率を戻します。
拡張一般化ガンマ分布の下側累積確率がpとなる分位点を戻します。mu、sigma、およびlambdaはそれぞれパラメータです。
Johnson Sb分布に従う確率変数がx以下になる確率を戻します。オプションの引数は、ガンマ（gamma）、デルタ（delta）、シータ（theta）、シグマ（sigma）です。Johnson Sb分布およびこれらのパラメータについては、『スクリプト構文リファレンス』の「JSL関数」章を参照してください。
Johnson Sb分布の下側累積確率がpとなる分位点を戻します。オプションの引数は、ガンマ（gamma）、デルタ（delta）、シータ（theta）、シグマ（sigma）です。Johnson Sb分布およびこれらのパラメータについては、『スクリプト構文リファレンス』の「JSL関数」章を参照してください。
Johnson Sb分布のxにおける密度を戻します。オプションの引数は、ガンマ（gamma）、デルタ（delta）、シータ（theta）、シグマ（sigma）です。Johnson Sb分布およびこれらのパラメータについては、『スクリプト構文リファレンス』の「JSL関数」章を参照してください。
Johnson Sl分布に従う確率変数がx以下になる確率を戻します。オプションの引数は、ガンマ（gamma）、デルタ（delta）、シータ（theta）、シグマ（sigma）です。Johnson Sl分布およびこれらのパラメータについては、『スクリプト構文リファレンス』の「JSL関数」章を参照してください。
Johnson Sl分布の下側累積確率がpとなる分位点を戻します。オプションの引数は、ガンマ（gamma）、デルタ（delta）、シータ（theta）、シグマ（sigma）です。Johnson Sl分布およびこれらのパラメータについては、『スクリプト構文リファレンス』の「JSL関数」章を参照してください。
Johnson Sl分布のxにおける密度を戻します。オプションの引数は、ガンマ（gamma）、デルタ（delta）、シータ（theta）、シグマ（sigma）です。Johnson Sl分布およびこれらのパラメータについては、『スクリプト構文リファレンス』の「JSL関数」章を参照してください。
Johnson Su分布に従う確率変数がx以下になる確率を戻します。オプションの引数は、ガンマ（gamma）、デルタ（delta）、シータ（theta）、シグマ（sigma）です。Johnson Su分布およびこれらのパラメータについては、『スクリプト構文リファレンス』の「JSL関数」章を参照してください。
Johnson Su分布の下側累積確率がpとなる分位点を戻します。オプションの引数は、ガンマ（gamma）、デルタ（delta）、シータ（theta）、シグマ（sigma）です。Johnson Su分布およびこれらのパラメータについては、『スクリプト構文リファレンス』の「JSL関数」章を参照してください。
Johnson Su分布のxにおける密度を戻します。オプションの引数は、ガンマ（gamma）、デルタ（delta）、シータ（theta）、シグマ（sigma）です。Johnson Su分布およびこれらのパラメータについては、『スクリプト構文リファレンス』の「JSL関数」章を参照してください。
対数一般化ガンマ分布に従う確率変数（パラメータmu、sigma、lambda）がxより小さい確率を戻します。
対数一般化ガンマ分布の下側累積確率がpとなる分位点を戻します。mu、sigma、およびlambdaはそれぞれパラメータです。
指定された相関をもつ2変量正規分布に従う確率変数(X,Y)が、(x,y)以下になる確率を計算します。XおよびYの平均と標準偏差をオプションで指定できます。平均のデフォルト値は0で、標準偏差のデフォルト値は1です。
グループ平均mean、グループ標準偏差stdev、およびグループ確率probabilityの正規混合分布のqにおける密度を戻します。mean、stdev、およびprobabilityの引数はすべて同じサイズのベクトルです。
グループ平均mean、グループ標準偏差stdev、およびグループ確率probabilityの正規混合分布に従う確率変数がqより小さい確率を戻します。mean、stdev、およびprobabilityの引数はすべて同じサイズのベクトルです。
SHASH（sinh-arcsinh）分布のxにおける密度を戻します。
SHASH（sinh-arcsinh）分布に従う確率変数がx以下になる確率を戻します。
SHASH（sinh-arcsinh）分布の累積確率pにおける分位点を戻します。
t分布の分位点（x）、自由度（DF）、およびオプションで非心度パラメータ（centered）を引数にとります。この関数は、与えられた引数を分布パラメータとした、分位点xにおける、Studentのt分布の密度を戻します。自由度5のt分布と、標準正規分布のグラフを描くには、まず、計算式Count(-3, 3, NRow())によって、分位点の列Xを作成します。2列目に、計算式t Density(X, 5)を挿入します。3列目に、計算式Normal Density(X)を挿入します。そして、［グラフ］>［重ね合わせプロット］を選んで、これらの密度をXに対してプロットします。このようなグラフを描くと、t分布は、正規分布より広がりが少し大きいことがわかります。
分位点（x）、自由度（DF）、および非心度パラメータ（centered）の3つを引数にとります。この関数は、指定された非心度パラメータと自由度を持つStudentのt分布の累積分布関数で、Studentのt分布に従う確率変数がx以下になる確率を戻します。たとえば、t Distribution(0.9, 5)は、自由度が5、非心度パラメータが0のStudentのt分布に従う確率変数が0.9以下である確率を戻します。この式は、0.79531を戻します。この関数には、自由度に整数でない数値も指定できます。非心度パラメータのデフォルト値は0ですが、任意の非心度パラメータの値を入力することもできます。t Quantile関数は、t Distribution関数の逆関数です。
t分布の生存確率(上側累積確率)の対数を戻します。
t分布の分位点xにおける確率密度の対数を戻します。
t分布の下側累積確率の対数を戻します。
prob=T Distribution (x, df, nc)となるような非心度パラメータncを求めます。
確率（p）、自由度（DF）、および非心度パラメータ（centered）の3つを引数にとります。この関数は、指定された非心度パラメータと自由度を持つStudentのt分布の分位点関数で、Studentのt分布の下側累積確率がpとなる分位点を戻します。 たとえば、t Quantile(0.95, 2.5)は、非心度パラメータが0で自由度2.5のStudentのt分布から95%点を戻します。この式は2.558219を戻します。t Quantile関数は、t Distribution関数の逆関数です。この関数は、自由度に整数でない数値も指定できます。非心度パラメータのデフォルト値は0ですが、任意の非心度パラメータの値を入力することもできます。t Distribution関数は、t Quantile関数の逆関数です。
Tukey HSD分布の分位点関数です。Tukeyの多重比較検定において、それ以下となる確率が(1-alpha)となる棄却値xを戻します。alphaは有意水準で、 nGroupsは検定のグループ数、 dfeは（すべての標本から計算される）誤差の自由度です。この棄却値は、Tukeyの多重比較検定で最小有意差を求めるのに使われます。
TukeyのHSD多重比較検定のp値を戻します。
Weibull分布の分位点、および、オプションで形状、尺度、閾値のパラメータを引数にとります。形状パラメータβ、尺度パラメータα、閾値パラメータθを持つWeibull分布の密度関数は、『基本的な統計分析』の「一変量の分布」章で取り上げられています。Weibull Density関数は、指定された分位点におけるWeibull分布の密度を戻します。
Weibull分布の値範囲にある分位点xの引数と、オプションで形状、尺度、閾値の引数を取ります。形状パラメータβ、尺度パラメータα、閾値パラメータθを持つWeibull分布の分布関数は、『基本的な統計分析』で取り上げられています。Weibull Distribution関数は、指定した形状・尺度・閾値パラメータを持つWeibull分布に従う確率変数がx以下になる確率を戻します。Weibull Distribution関数は、Weibull Quantile関数の逆関数です。
Weibull分布は、尺度パラメータ（αと表すことが多い）と形状パラメータ（βと表すことが多い）の値によって分布の形が決まり、 特に機械装置や生物学上の寿命を推定するときのモデルとしてよく使用されます。2パラメータWeibull分布は、閾値が0に指定された3パラメータWeibull分布と同じです。
指定された形状パラメータ（shape）、尺度パラメータ（scale）、閾値パラメータ（threshold）を持つWeibull分布において、累積確率pに対する分位点を戻します。Weibull Quantile関数は、Weibull Distribution関数の逆関数です。