Y의 Box-Cox 변환
"최소 제곱 적합" 보고서의 "Y의 Box-Cox 변환" 옵션을 선택하면 정규성 및 등분산성에 대한 일반적인 회귀 가정이 더 잘 만족되도록 반응을 변환할 수 있습니다. 그런 다음 회귀 모형을 사용하여 변환된 반응을 적합시킬 수 있습니다. 그러나 다른 이유로 변수를 변환할 때도 Box-Cox 멱 변환을 사용할 수 있습니다. 이 변환은 반응 Y가 순양수인 경우에만 적합합니다.
일반적으로 사용되는 변환은 반응을 지정된 횟수만큼 거듭제곱합니다. Box and Cox(1964)에서는 이러한 멱 변환 계열을 공식화하고 기술했습니다. 변환 계산식은 모수 l로 표현된 연속 정의를 제공하고 오차 제곱합을 비교할 수 있도록 구성되었습니다. 구체적으로, 다음 방정식을 사용하여 변환 계열을 제공합니다.
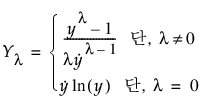
여기서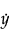 
는 기하평균을 나타냅니다.
"Y의 Box-Cox 변환" 옵션은 l = –2에서 2까지 0.2 단위로 증가하여 변환을 적합시킵니다. l 값을 선택하기 위해 이러한 각 변환에 대한 가능도 함수가 계산됩니다. 이 함수는 오차가 독립적이며 평균이 0, 분산이 s2인 정규 분포를 따른다고 가정하여 계산됩니다. 가능도를 최대화하는 l 값이 선택됩니다. 또한 이 값은 l 값에 대해 SSE를 최소화합니다. SSE를 최소화하는 l 값은 SSE가 가장 작은 격자 점을 둘러싼 두 증분 격자점 사이의 2차 보간을 사용하여 구합니다. 이 보간법으로 인해 SSE 값이 음수가 되면 SSE를 최소화하는 l의 격자 값이 최선의 l로 보고됩니다.
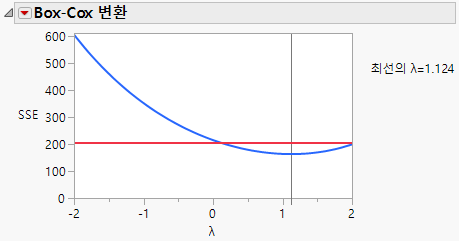
"Box-Cox 변환" 보고서에는 l 값에 대한 SSE(오차 제곱합) 값을 보여 주는 그림이 표시됩니다. 그림의 빨간색 수평선은 l에 대한 단측 95% 신뢰 구간을 나타냅니다. 이 신뢰 구간은 Box and Cox(1964, p. 216)에 정의된 신뢰 영역을 기반으로 합니다. 신뢰 영역은 다음 부등식으로 정의됩니다.
SSE(l) < SSE(lbest) * exp(ChiSquareQuantile(0.95,1) / dfe)
다음은 각 요소에 대한 설명입니다.
SSE(lbest)는 보고된 최선의 l를 사용하여 계산된 SSE입니다.
ChiSquareQuantile(0.95,1)은 자유도가 1인 c2 분포의 0.95번째 분위수입니다.
dfe는 회귀 모형에 대한 분산 분석 테이블의 오차 자유도입니다.
"Box-Cox 변환" 보고서에서는 다음 옵션을 제공합니다.
변환을 사용한 재적합
변환된 Y 변수를 정의하기 위한 람다 값을 지정한 다음, 변환된 변수에 대한 최소 제곱 적합을 제공할 수 있습니다.
변환으로 바꾸기
변환된 Y 변수를 정의하기 위한 람다 값을 지정한 다음, 기존 최소 제곱 적합을 변환된 변수에 대한 적합으로 바꿀 수 있습니다. 반응이 여러 개인 경우 "변환으로 바꾸기"는 변환 대상 반응에 대한 보고서만 바꿉니다.
최적 변환 저장
데이터 테이블에 새 열을 생성하고 최적 변환을 위한 계산식을 저장합니다.
특정 변환 저장
람다 값을 지정하고, 지정된 변환을 위한 계산식이 포함된 열을 데이터 테이블에 생성할 수 있습니다.
추정값 테이블
–2에서 2까지 0.2 단위로 증가하는 모든 l에 대한 모수 추정값 및 SSE 값을 포함하는 새 데이터 테이블을 생성합니다.
Figure 3.37의 그림에서는 최선의 l 값이 0.1과 2.0 사이임을 보여 줍니다. JMP가 l 값의 0.2 단위 격자에서 최적 값 두 개 사이의 보간을 사용하여 선택한 값은 1.124입니다.
팁: Box-Cox 변환 그림을 생성하는 데 사용된 SSE 값을 확인하려면 "Box-Cox 변환"의 빨간색 삼각형 메뉴에서 "추정값 테이블" 옵션을 사용합니다.
그림 3.37 Y의 Box-Cox 변환
