만족도 함수 생성
예측 프로파일러에 추가되는 개별 만족도 함수는 세 개의 정의 점을 통과하는 조각별 평활 함수입니다. 이러한 점을 관리점(낮음, 중간, 높음)이라고 하며 만족도 함수의 모양을 대화식으로 제어하는 데 사용할 수 있습니다.
• "최소화" 및 "최대화" 함수는 관리점과 꼬리의 지수 사이에 3차를 보간하는 세 부분으로 구성된 조각별 평활 함수입니다.
• "목표값 일치" 함수는 중간 값의 양쪽 편에 있는 정규 밀도의 척도 배수인 조각별 함수(각각 다른 곡선)이며, 조각별로 평활 후 관리점에 적합됩니다. 지수 함수가 꼬리에 적합됩니다.
• "없음" 함수를 사용하면 임의의 만족도 함수를 지정할 수 있습니다. 특히 만족도를 "낮음" 및 "높음" 값보다 "중간" 값에서 더 낮게 지정할 수 있습니다. 계산식을 사용하여 사용자 만족도 함수를 생성할 수도 있습니다. 자세한 내용은 사용자 정의 만족도 함수에서 확인하십시오.
"낮음" 및 "높음" 관리점은 0 또는 1까지 도달할 수 없습니다. 만족도 함수를 생성하는 이 방법은 만족도 값이 최대화, 목표값 일치 및 최소화 사이에서 전환되므로 양호한 동작을 수행합니다.
참고: JMP는 Derringer & Suich(1980) 함수 형식을 사용하지 않습니다. 이 형식은 평활 함수가 아니므로 JMP의 최적화 알고리즘과 잘 작동하지 않을 때도 있습니다.
다중 최적화를 위한 만족도 함수
다중 반응을 최적화해야 할 경우 전체 만족도 함수가 생성되고 최적화됩니다. 모든 반응에 대한 전체 만족도는 개별 반응에 대한 만족도 함수의 기하평균으로 정의됩니다.
k개 반응에 대한 개별 만족도 함수를 d1, d2,...,dk로 나타냅니다. 그러면 전체 만족도 함수는 다음과 같이 개별 만족도 함수의 기하평균입니다.
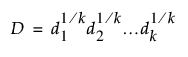
"중요도" 값이 "반응 한계" 열 특성의 일부로 지정되거나 "반응 목표" 창에서 정의된 경우 전체 만족도 함수에 통합됩니다. "중요도" 값은 합이 1이 되도록 조정됩니다. 크기가 조정된 중요도 값을 w1, w2,..., wk로 나타냅니다. 그러면 전체 만족도는 다음과 같이 개별 만족도 함수의 가중 기하평균으로 정의됩니다.
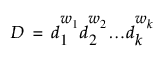
최적화 알고리즘
전체 만족도 함수 또는 단일 만족도 함수(반응이 하나뿐인 경우)의 최적화에 사용되는 방법은 요인 유형에 따라 다릅니다.
• 범주형 요인의 경우 좌표 교환 알고리즘이 사용됩니다.
• 연속형 요인의 경우 경사하강법 알고리즘이 사용됩니다.
• 제약 조건 또는 혼합물 요인이 있는 경우 Wolfe 그래디언트 축소 방법이 사용됩니다.
• 로컬 최적 해를 찾을 위험을 줄이기 위해 JMP에서는 다중 랜덤 시작을 사용합니다.