추정값 상관계수
"최소 제곱 적합" 보고서의 "추정값 상관계수" 옵션은 모수 추정값에 대한 상관 행렬을 계산합니다. 이러한 상관은 공선성이 있는지 여부를 나타냅니다.
이 행렬의 생성에 대한 이해를 위해 일반적인 최소 제곱 회귀 공식을 고려합니다. 여기서 반응(Y)은 예측 변수(x’s) + 오차(e)의 선형 함수입니다.
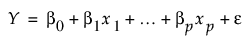
데이터 테이블의 각 행에는 반응 값 및 p 예측 변수의 값이 포함됩니다. 각 관측값에 대해 예측 변수 값은 고정 값으로 간주됩니다. 그러나 반응 값은 확률 변수의 실현값으로 간주됩니다.
고정된 예측 변수 값을 고려하면 Y 값 집합에 대해 b0, b1, ¼, bp 계수를 추정할 수 있습니다. 일반적으로 Y 값 집합이 다르면 계수 추정값이 다릅니다. "추정값 상관계수" 옵션은 이러한 모수 추정값의 이론적 상관계수를 계산합니다. 기술 상세 정보는 사용자 검정 예에 대한 통계 상세 정보에서 확인하십시오.
모수 추정값의 상관계수는 예측 변수 값과 절편을 나타내는 항에만 의존합니다. 두 모수 추정값 간의 상관계수는 반응 값의 영향을 받지 않습니다.
두 추정값 간에 높은 양의 상관관계가 있으면 해당하는 두 예측 변수 간에 공선성 관계가 존재할 수 있음을 나타냅니다. 그러나 이러한 상관관계를 주의하여 해석해야 합니다(Belsley et al. 1980, p. 185, 92–94). 또한 예측 변수를 재조정하여 평균이 변화되면 모수 추정값과 절편 값의 상관관계가 변경됩니다.
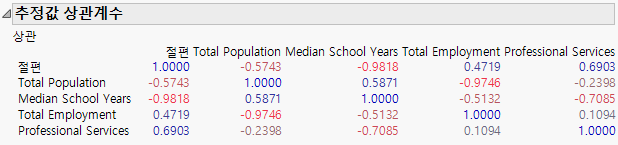
그림 3.25 추정값 상관계수 보고서
Figure 3.25의 "추정값 상관계수" 보고서에서는 절편과 Median School Years의 모수 추정값 간에 높은 음의 상관관계가 있음을 보여 줍니다(–0.9818). Total Population과 Total Employment 간에도 높은 음의 상관관계가 있습니다(–0.9746).