반복 측정의 예
반복 측정의 예
두 가지 신약이 콜레스테롤 수치를 낮추는 데 효과가 있는지, 그리고 시간과 치료 간에 상관관계가 있는지 여부를 판별하기 위해 모형 적합 플랫폼을 사용하여 반복 측정 혼합 모형을 적합시키려고 합니다. 대조 약물에 대해 두 가지 새 콜레스테롤 약물을 테스트하기 위한 연구가 수행되었습니다. 콜레스테롤 수치가 높은 20명의 환자를 각각 네 가지 치료(두 가지 실험 약물, 대조 약물, 플라시보)에 무작위로 할당했습니다. 연구 기간 동안 각 환자의 총 콜레스테롤 수치를 6번 측정했습니다(4월 1일, 5월 1일, 6월 1일 아침과 오후 한 번씩).
 배경
배경
일반적으로 이러한 설계를 분석하기 위해 다음과 같은 두 가지 방법이 사용되었습니다.
• MANOVA(다변량 분산분석)
• 수정된 Huynh-Feldt(1976) 또는 Greenhouse-Geisser(1959) 연구 자료를 사용한 시간 단변량 ANOVA(분산 분석)의 분할구
두 옵션 모두 모형 적합의 다변량 분산분석을 통해 사용할 수 있습니다. 이러한 양극단 두 옵션은 공분산 구조를 모델링하기 위한 것입니다. 다변량 분산분석에서는 모든 변수와 공분산이 개별적으로 추정되는 비정형 공분산 구조를 가정합니다. 시간 분석의 독립 분할구에서는 모든 오차가 독립적이라고 가정합니다. 이는 가우시안 데이터에 대해 복합 대칭 공분산 구조를 가정하는 것에 해당합니다.
이 두 모형은 처리 효과에 대해 상당히 다른 결론을 내릴 수 있습니다. 복소 공분산 구조를 가정하면 데이터의 정보를 사용하여 공분산 모수를 추정합니다. 너무 많은 공분산 모수를 적합시키면 모형 과대적합이 발생할 위험이 있습니다. 반복 측정 데이터를 모델링하는 경우 이러한 문제를 상쇄하는 공분산 구조를 찾아야 합니다.
• 모형이 과대적합되면 덜 복잡한 공분산 구조를 가정할 때보다 차이를 감지하는 검정력이 더 작습니다.
• 모형이 과소적합되면 제1종 오류 제어가 손실됩니다. 경우에 따라 기각률이 부풀려질 수도 있습니다. 그렇지 않은 경우 분산 팽창으로 인해 기각률이 감소합니다.
 공분산 구조
공분산 구조
혼합 모형 분석법은 다양한 공분산 구조를 적합시킵니다. 시간에 따른 반복 측정의 경우 대개 Toeplitz 공분산 구조와 AR(1)(1차 자기회귀) 공분산 구조 모두 적절한 상관 구조를 제공합니다. 이러한 구조는 모형을 과대적합시키지 않고도 상관관계가 있는 관측값을 허용합니다. AR(1)은 공통 분산 모수를 가정하는 반면, 이분산을 사용한 Toeplitz 공분산 행렬은 반복 측정 변수의 각 단위에 대해 고유한 분산을 추정합니다. 자세한 내용은 반복 공분산 구조 요구 사항에서 확인하십시오.
이 예에서는 네 가지 공분산 구조를 적합시킵니다. 관측 시간 수 J는 6입니다.
• 공분산 구조: 비정형. 비정형 모형은 모든 공분산 모수(J(J+1)/2)를 합하여 적합시킵니다. 이 예에서 모형은 21개의 분산을 적합시킵니다.
• 공분산 구조: 잔차. 잔차 모형은 일반적인 분산 성분 구조와 동등합니다. 이 예에서 모형은 두 개의 분산을 적합시킵니다.
• 공분산 구조: Toeplitz. Toeplitz 모형은 2J-1개의 공분산 모수를 적합시킵니다. 이 예에서 모형은 11개의 분산을 적합시킵니다.
• 공분산 구조: AR(1). 이 모형은 두 개의 공분산 모수를 적합시킵니다. 한 모수는 분산을 결정하고 다른 모수는 시간에 따라 공분산이 어떻게 변하는지 결정합니다.
AICc를 사용하여 모형 적합을 평가합니다. BIC 기준도 사용할 수 있습니다. 이 경우 두 기준에 의해 선택된 모형이 동일합니다. 최적의 공분산 구조를 선택한 후 추가 분석을 계속합니다.
팁: 이 예를 진행하는 동안 모형 적합 시작 창을 열어 두십시오.
 데이터 구조
데이터 구조
Cholesterol.jmp 데이터 테이블은 반복 측정 데이터를 기록하는 데 일반적으로 사용되는 형식으로 되어 있습니다. 혼합 모형 분석법을 사용하여 이러한 데이터를 분석하려면 각 콜레스테롤 측정값이 Cholesterol Stacked.jmp와 같이 고유의 행에 포함되어야 합니다. Cholesterol Stacked.jmp를 구성하기 위해 테이블 > 쌓기를 사용하여 Cholesterol.jmp의 데이터를 쌓았습니다.
쌓인 테이블의 Days 열은 계산식을 사용하여 생성되었습니다. Days 열은 콜레스테롤 수치를 측정한 시간(일 수)을 연구에 제공합니다. 모델링 유형은 연속형입니다. AR(1) 공분산 구조에는 반복 효과가 연속형이어야 하므로 이 유형이 필요합니다.
 공분산 구조: 비정형
공분산 구조: 비정형
먼저 비정형 공분산 구조를 사용하여 모형을 적합시킵니다.
1. 도움말 > 샘플 데이터 폴더를 선택하고 Cholesterol Stacked.jmp를 엽니다.
2. 분석 > 모형 적합을 선택합니다.
3. 다음 예에서 시작 창으로 돌아갈 수 있도록 대화상자 열린 채 유지를 선택합니다.
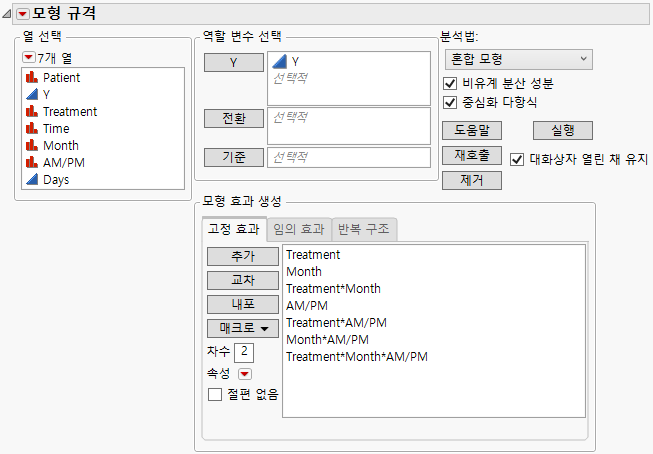
4. Y를 선택하고 Y를 클릭합니다.
5. "분석법" 목록에서 혼합 모형을 선택합니다.
6. Treatment, Month, 및 AM/PM을 선택한 후 매크로 > 완전 요인을 선택합니다.
그림 8.12 완료된 고정 효과 탭을 보여 주는 모형 적합 시작 창
7. 반복 구조 탭을 선택합니다.
8. "구조" 목록에서 비정형을 선택합니다.
9. Time을 선택하고 반복을 클릭합니다. 반복 열은 개체 내에서 반복 측정을 정의합니다.
10. Patient를 선택하고 개체를 클릭합니다.
참고: 비정형 공분산 모형에서는 반복 구조 변수가 중복 값을 가질 수 없습니다. 이 예에서는 개체가 치료(treatment)에 내포되고, 각 치료 내에서 1, 2, 3, 4, 5 값을 사용하여 환자(patient)에 번호가 매겨져 있다고 가정합니다. 이 분석을 실행하면 경고가 표시됩니다. 반복 변수의 각 값에 서로 다른 식별자를 지정하기 위해 환자 번호를 다시 매겨야 합니다. 또는 데이터 테이블에 치료 내의 내포를 나타내는 열을 생성하고 이 효과를 개체로 입력해야 합니다.
그림 8.13 완료된 반복 구조 탭을 보여 주는 모형 적합 시작 창
11. 실행을 클릭합니다.
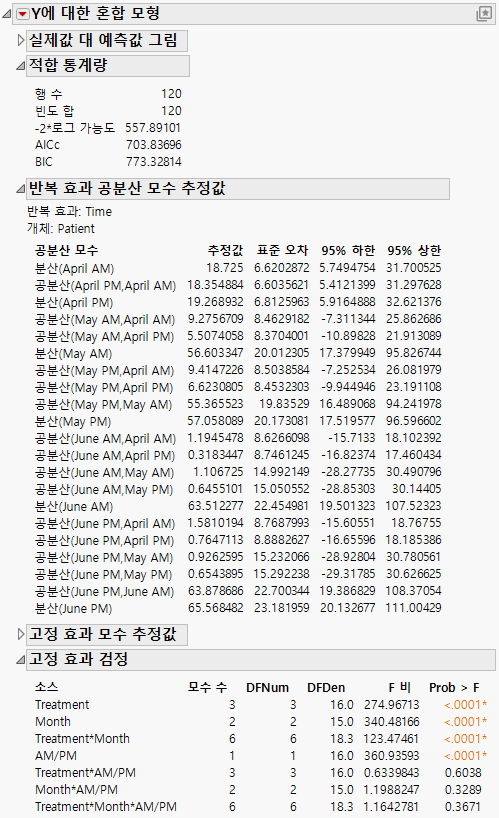
Figure 8.14에 "혼합 모형" 보고서가 표시되어 있습니다. AICc 또는 BIC를 사용하여 세 가지 모형을 비교하려고 하므로 "적합 통계량" 보고서를 확인해야 합니다. 비정형 모형의 AICc는 703.84입니다.
"반복 효과 공분산 모수 추정값" 보고서에서는 21개의 모든 공분산 모수에 대한 추정값을 보여 줍니다. 예상대로 더 가까운 시간의 관측값이 더 멀리 떨어진 관측값보다 공분산이 큽니다. 또한 시간에 따라 분산이 증가합니다.
그림 8.14 비정형 공분산 구조에 대한 혼합 모형 보고서
 공분산 구조: 잔차
공분산 구조: 잔차
잔차 공분산 구조는 분할구 모형을 적합시킬 때 적절합니다.
1. 공분산 구조: 비정형에 나오는 step 1 ~ step 7를 완료합니다.
2. 반복 구조 탭의 "구조" 목록에서 잔차를 선택합니다.
3. 이전 예에서 계속하는 경우 Time과 Patient를 제거합니다.
그렇지 않으면 "잔차 반복 공분산 구조를 선택한 경우에는 반복 열 및 개체 열이 무시됩니다"라는 경고가 표시됩니다. 확인을 클릭하여 분석을 계속할 수도 있습니다.
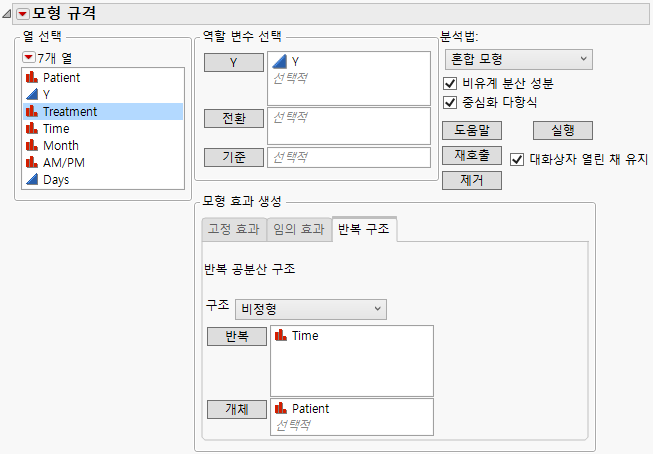
4. 임의 효과 탭을 선택합니다.
5. Patient를 선택하고 추가를 클릭합니다.
6. "임의 효과" 영역에서 Patient를 선택하고 Treatment 열을 선택한 후 내포를 클릭합니다.
그림 8.15 완료된 임의 효과 탭을 보여 주는 모형 적합 시작 창
7. 실행을 클릭합니다.
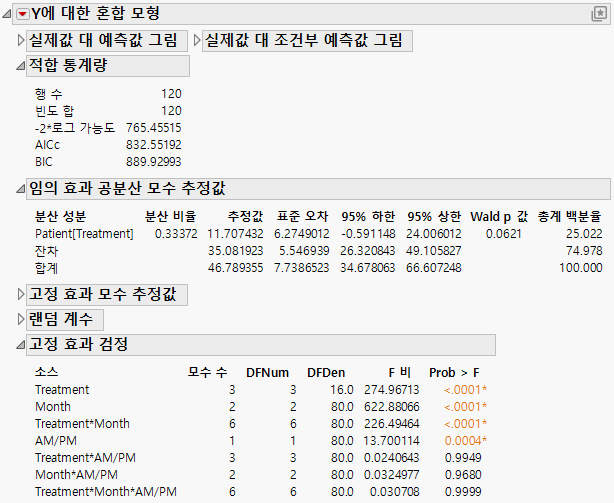
Figure 8.16에 "혼합 모형" 보고서가 표시되어 있습니다. "적합 통계량" 보고서에 따르면 잔차 모형의 AICc는 832.55이며 이는 비정형 모형의 703.84와 비교됩니다.
"임의 효과 공분산 모수 추정값" 보고서에는 두 공분산 모수의 추정값이 표시됩니다. 이러한 값은 Treatment에 내포된 Patient의 분산 및 잔차 분산의 추정값입니다.
그림 8.16 잔차 오차 공분산 구조에 대한 혼합 모형 보고서
 공분산 구조: Toeplitz
공분산 구조: Toeplitz
Toeplitz 이분산 구조를 사용하여 모형을 적합시킵니다.
1. 공분산 구조: 비정형에 나오는 step 1 ~ step 6를 완료합니다.
2. 이전 예에서 계속하는 경우 임의 효과 탭의 Patient[Treatment]를 선택한 후 제거를 클릭합니다.
임의 효과와 반복 효과를 모두 포함하면 데이터가 부족하여 효과를 둘 다 추정하지 못하는 경우가 많습니다.
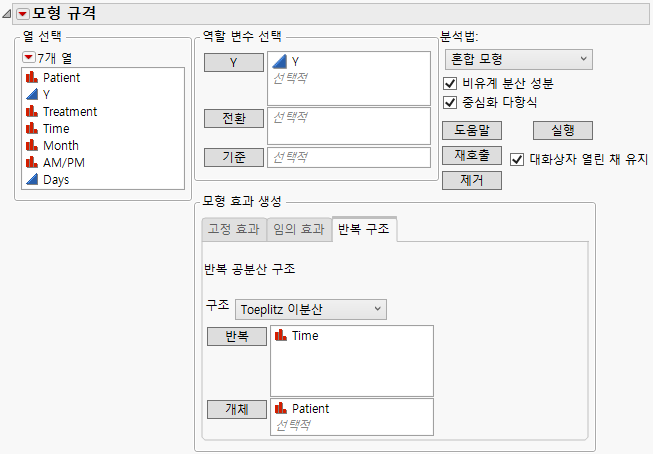
3. 반복 구조 탭을 선택합니다.
4. "구조" 목록에서 Toeplitz 이분산을 선택합니다.
5. Time을 선택하고 반복을 클릭합니다.
6. Patient를 선택하고 개체를 클릭합니다.
그림 8.17 완료된 반복 구조 탭을 보여 주는 모형 적합 시작 창
7. 실행을 클릭합니다.
그림 8.18 Toeplitz 이분산 구조에 대한 혼합 모형 보고서
참고: JMP의 혼합 모형 분석법은 상관관계를 보고하는 반면 SAS의 PROC MIXED는 공분산을 보고합니다.
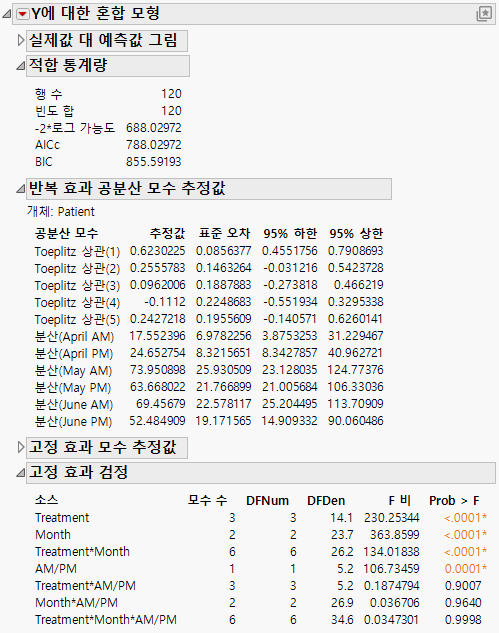
"적합 통계량" 보고서에 따르면 이분산을 사용한 Toeplitz 모형의 AICc는 788.03입니다. 이 값을 잔차 모형의 832.55 및 비정형 모형의 703.84와 비교합니다.
Toeplitz 이분산 구조를 사용하는 경우 11개의 공분산 모수를 추정해야 합니다. 이러한 추정값은 "반복 효과 공분산 모수 추정값" 보고서에 표시됩니다. Toeplitz 상관 추정값 다음에 각 시점에 대한 분산 추정값이 나옵니다. 이 행렬이 파라미터화되는 방법에 대한 자세한 내용은 반복 측정에 대한 통계 상세 정보에서 확인하십시오.
 공분산 구조: AR(1)
공분산 구조: AR(1)
마지막으로 AR(1) 구조를 적합시킵니다.
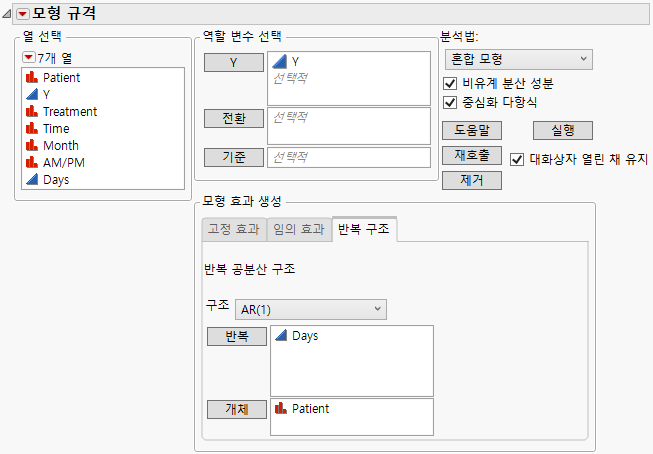
1. 공분산 구조: 비정형에 나오는 step 1 ~ step 6를 완료합니다.
2. 이전 예에서 계속하는 경우 반복 상자의 Time을 선택한 후 제거를 클릭합니다.
AR(1)을 사용하는 경우 반복 값에 대한 변수가 연속형이어야 합니다.
3. "구조" 목록에서 AR(1)을 선택합니다.
4. Days를 선택하고 반복을 클릭합니다.
그림 8.19 완료된 반복 구조 탭을 보여 주는 모형 적합 시작 창
5. 실행을 클릭합니다.
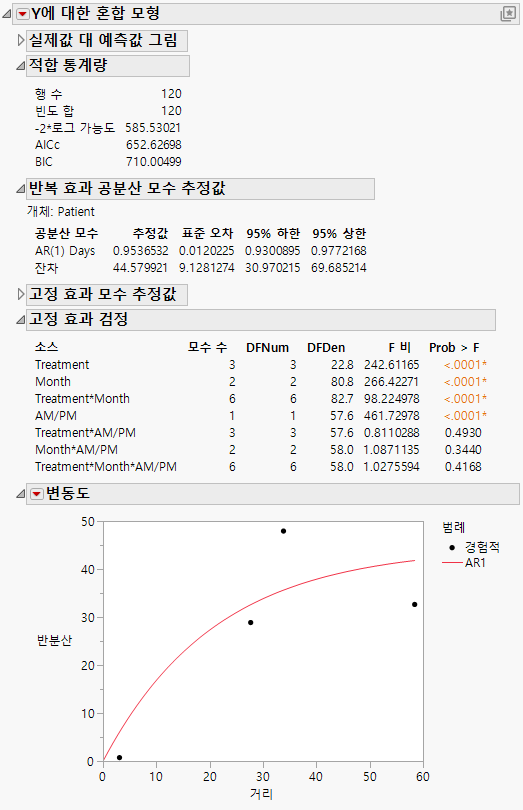
Figure 8.20에 "혼합 모형" 보고서가 표시되어 있습니다. "적합 통계량" 보고서에 따르면 AR(1) 모형의 AICc는 652.63입니다. 이 값을 잔차 모형의 832.55, 비정형 모형의 703.84 및 Toeplitz 이분산 모형의 788.03과 비교합니다. AICc 기준에 따르면 AR(1) 모형이 네 개 모형 중 가장 적합합니다.
AR(1) 구조를 사용하는 경우 두 개의 공분산 모수를 추정해야 합니다. 이러한 추정값은 "반복 효과 공분산 모수 추정값" 보고서에 표시됩니다. AR(1) Days 모수 추정값은 AR(1) 구조의 상관 모수인 r의 추정값입니다.
변동도 그림에는 AR(1) 모형에 대한 경험적 반분산과 곡선이 표시됩니다. Days에는 0이 아닌 값이 5개뿐이므로 4개의 거리 클래스만 가능하고 4개의 점만 표시됩니다. AR(1) 구조는 적절해 보입니다. 다른 구조를 탐색하려면 "변동도"의 빨간색 삼각형 메뉴에서 옵션을 선택합니다. "변동도" 옵션에 대한 자세한 내용은 변동도에서 확인하십시오.
그림 8.20 AR(1) 공분산 구조에 대한 혼합 모형 보고서
 AR(1) 구조를 사용한 추가 분석
AR(1) 구조를 사용한 추가 분석
AR(1) 모형이 최량 적합을 제공하므로 이 모형을 채택하여 분석을 계속합니다. "고정 효과 검정" 보고서에서는 AM/PM의 주효과뿐만 아니라 Treatment와 Month 간에 유의한 교호작용이 있음을 나타냅니다. 이제 이러한 유의 효과에 대해 살펴보겠습니다.
1. "혼합 모형"의 빨간색 삼각형을 클릭하고 주변 모형 추론 > 프로파일러를 선택합니다.
"주변 모형 프로파일러" 보고서(Figure 8.21)를 사용하면 Treatment, Month 및 AM/PM의 다양한 설정이 콜레스테롤 수준(Y)에 미치는 영향을 확인할 수 있습니다.
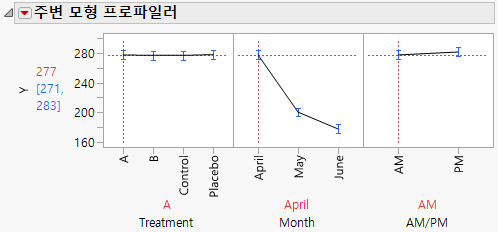
2. Month 그림에서 빨간색 수직 점선을 April에서 May로 드래그한 후 June으로 드래그합니다.
3개월 동안 Y에 대한 예측 AM 측정값이 277.4(April 평균)에서 177.7(June 평균)로 감소합니다.
3. Treatment 그림에서 빨간색 수직 점선을 A에서 B로 드래그합니다.
Month 그림의 선을 April에서 June으로 드래그하면 Treatment B의 경우 Y에 대한 예측 AM 평균이 276.8(April)에서 191.2(June)로 감소하는 것을 볼 수 있습니다.
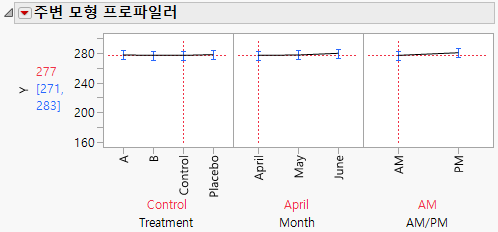
4. Treatment 그림에서 수직 점선을 Control로 드래그한 후 Placebo로 드래그합니다.
Treatment를 Control 또는 Placebo로 설정하면 3개월 동안 거의 변화가 없습니다(Figure 8.22).
다음으로 AM/PM 효과를 살펴봅니다.
5. 빨간색 수직선을 드래그하여 Treatment와 Month를 12개의 모든 수준 조합으로 설정합니다.
12개의 모든 조합에 대해 예측 콜레스테롤 수준은 일관되게 아침보다 오후에 더 높아 주효과를 설명합니다.
Treatment A는 Treatment B보다 5월(May)에 콜레스테롤 수치가 더 낮은 것으로 보입니다. 이 효과가 유의하면 Treatment A가 B보다 빨리 반응한다고 할 수 있습니다. 다음 섹션 6월(June)의 모든 치료(Treatment) 비교에서는 치료(Treatment)를 평가하는 방법을 보여 줍니다.
그림 8.21 Treatment A에 대한 주변 프로파일러 그림
그림 8.22 Control에 대한 주변 프로파일러 그림
6월(June)의 모든 치료(Treatment) 비교
연구는 4월(April), 5월(May), 6월(June)에 걸쳐 수행됩니다. 6월(June)의 PM 측정에서 어떤 치료법이 차이가 있는지 알아보려고 합니다.
1. "혼합 모형"의 빨간색 삼각형을 클릭하고 다중 비교를 선택합니다.
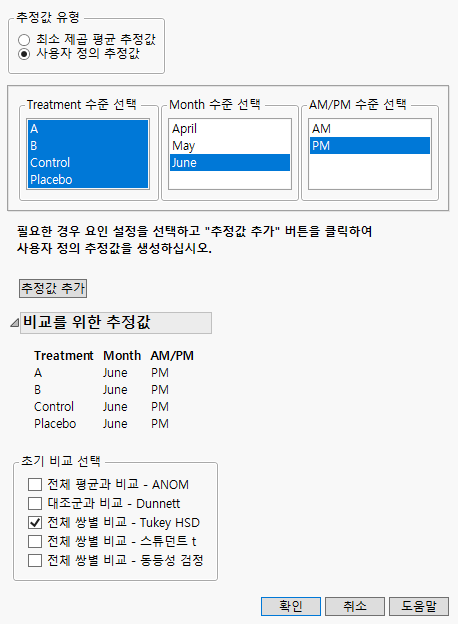
2. "추정값 유형"에서 사용자 정의 추정값을 선택합니다.
3. "Treatment 수준 선택" 패널에서 네 가지 치료 유형을 모두 선택합니다.
4. "Month 수준 선택" 패널에서 "June"을 선택합니다.
5. "AM/PM 수준 선택" 패널에서 "PM"을 선택합니다.
6. 추정값 추가를 클릭합니다.
7. "초기 비교 선택" 목록에서 전체 쌍별 비교 - Tukey HSD를 선택합니다.
그림 8.23 완료된 다중 비교 창
8. 확인을 클릭합니다.
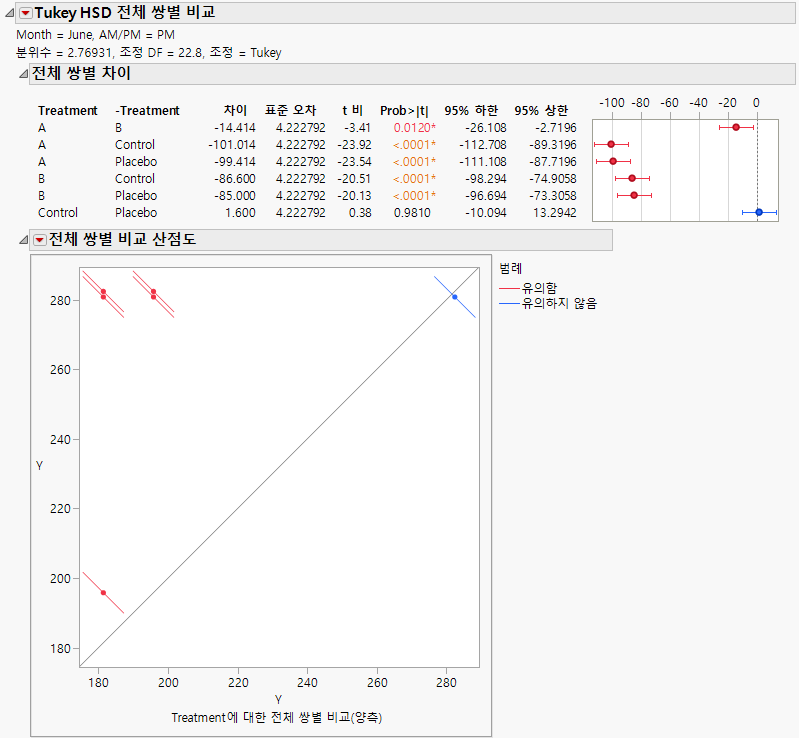
그림 8.24 June PM의 모든 Treatment에 대한 Tukey HSD 전체 쌍별 비교 보고서
"Tukey HSD 전체 쌍별 비교" 보고서에는 "전체 쌍별 차이" 보고서와 "전체 쌍별 비교 산점도"가 표시됩니다. June PM 측정에 대해 Control과 Placebo를 제외한 모든 치료가 유의하게 다릅니다.
치료 A와 B 간의 차이를 검토합니다. 평균 차이는 -14.414이고 신뢰 구간 범위는 -26.108 ~ -2.7196입니다. 치료 A에 의한 콜레스테롤 측정값 감소가 치료 B에 의한 감소보다 2.7 ~ 26.1점 정도 높다는 결론을 내릴 수 있습니다. 치료 A와 B 둘 다 Control과 Placebo에 비해 매우 효과적입니다.
 AR(1)에 대한 회귀 모형의 예
AR(1)에 대한 회귀 모형의 예
Month 및 AM/PM 범주형 효과를 사용하여 콜레스테롤 데이터에 대한 네 가지 공분산 구조를 비교했습니다. 비정형 적합을 위해 범주형 효과가 필요했습니다. 결과적으로 AR(1) 공분산 구조를 사용하기로 결정했습니다.
이제 범주형 효과 대신 연속형 효과 Days를 사용하여 치료 효과를 모델링한다고 가정해 보겠습니다. 그런 다음 치료 기간 동안 임의의 시간에서 콜레스테롤 수준을 예측할 수 있습니다.
1. 공분산 구조: AR(1)에서 step 1 ~ step 4를 수행한 후 모형 적합 시작 창으로 돌아갑니다.
2. "고정 효과" 탭에서 기존 고정 효과를 선택하고 제거를 클릭합니다.
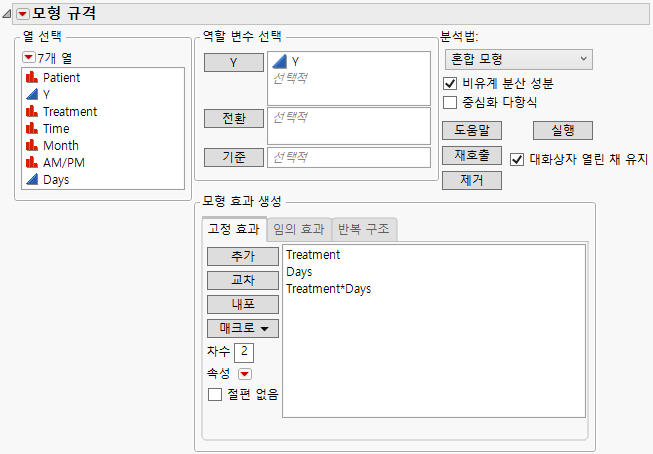
3. Treatment와 Days를 선택한 후 매크로 > 완전 요인을 선택합니다.
그림 8.25 고정 효과 탭을 보여 주는 모형 적합 시작 창
4. "모형 규격"의 빨간색 삼각형을 클릭하고 중심화 다항식을 선택 취소합니다.
참고: 기본 설정에서는 교호작용 항에 사용되는 연속형 효과가 중심화됩니다. "중심화 다항식" 옵션을 해제하면 교호작용 항의 연속형 효과가 중심화되지 않습니다.
5. 실행을 클릭합니다.
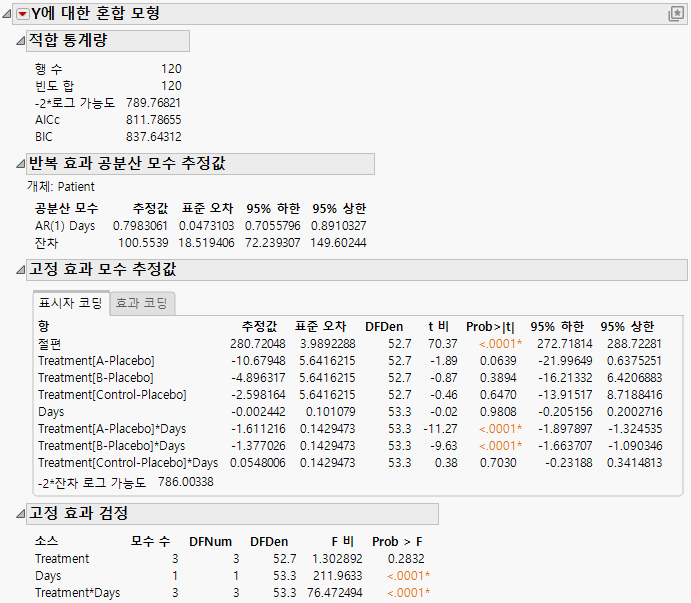
Figure 8.26에 "혼합 모형" 보고서가 표시되어 있습니다. Treatment와 Days의 교호작용이 매우 유의하며 약물에 대해 다양한 회귀를 나타낸다는 것을 확인할 수 있습니다.
참고: 다른 날짜의 약물에 대한 결과를 예측하려면 프로파일러를 사용합니다. 자세한 내용은 프로파일러의 프로파일러에서 확인하십시오.
그림 8.26 연속형 고정 효과를 사용하는 AR(1) 공분산 구조에 대한 혼합 모형 보고서