최적 기준
사용자 설계는 최적 기준에 따라 달라지는 검색 루틴을 사용하여 생성됩니다. 이 섹션에서는 사용자 설계 생성을 위한 최적 기준에 대한 정보를 제공합니다.
• 권장 사항
• D-최적
• I-최적
• A-최적
• 별칭 최적
권장 사항
주효과 및 2요인 교호작용에 대한 2수준 설계의 경우 A-최적, RSM 버튼을 사용하여 생성된 완전 2차 모형의 경우 I-최적, 나머지 경우에는 D-최적을 각각 지정합니다.
D-최적
D-최적 기준은 모형 계수 추정값의 공분산 행렬에 대한 행렬식을 최소화합니다. 결과적으로 D-최적은 효과의 정확한 추정에 중점을 둡니다. 이 기준은 다음과 같은 경우에 적합합니다.
• 선별 설계
• 효과 추정 또는 유의성 검정에 중점을 둔 실험
• 활성 요인 식별이 실험 목표인 설계
D-최적 기준은 가정된 모형에 종속됩니다. 참모형의 형태를 미리 알 수 없는 경우가 많아서 이 제한이 있습니다. D-최적 설계의 런은 가정된 모형의 계수 정밀도를 최적화합니다. 극단적으로 D-최적 설계는 런 수가 모수와 동일하고 적합 결여의 자유도가 없는 포화 상태일 수 있습니다.
특히 D-최적 설계는 D를 최대화합니다. 여기서 D는 다음과 같이 정의됩니다.
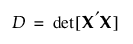
X는 반응 시뮬레이션에 정의된 모형 행렬입니다.
D-최적 분할구 설계는 D를 최대화합니다. 여기서 D는 다음과 같이 정의됩니다.
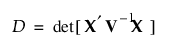
V -1은 반응에 대한 공분산 행렬의 대각 블록입니다(Goos 2002).
D-최적 설계는 계수의 표준 오차를 최소화하는 데 중점을 두기 때문에 모형이 올바른지 확인하지 못할 수 있습니다. 예를 들어 D-최적 설계에는 1차 모형의 중앙점이 포함되지 않습니다. 가정된 모형에 포함되지 않은 잠재적 활성 항이 있는 경우 If Possible 항을 지정하고 베이지안 D-최적 설계를 사용하는 것이 더 좋은 방법입니다.
베이지안 D-최적
베이지안 D-최적은 수정된 D-최적 기준입니다. 베이지안 D-최적 기준은 잠재적 활성 교호작용 또는 비선형 효과가 있을 때 유용합니다. 자세한 내용은 DuMouchel and Jones(1994) 및 Jones et al(2008)에서 확인하십시오.
베이지안 D-최적은 지정된 모형 모수 집합을 정확하게 추정합니다. 이는 "모형" 섹션에서 "추정 가능성"을 "필수"로 지정한 효과입니다. 그러나 이와 동시에 베이지안 D-최적은 런 크기에서 허용하는 대로 다른 효과(대개 고차 효과)를 추정할 수 있습니다. 이는 "모형" 섹션에서 "추정 가능성"을 "If Possible"로 지정한 효과입니다. 런 크기 제한이 주어졌을 때 베이지안 D-최적 설계는 필수 효과만 포함된 모형에서 부적합성을 감지할 수 있습니다.
베이지안 D-최적 기준은 런 수가 "필수" 항의 수보다 많지만 "필수" 항과 "If Possible" 항의 합보다 작을 때 가장 효과적입니다. 이 경우 런 수는 추정할 모수의 수보다 적습니다. 베이지안 설정의 사전 정보를 사용하면 모든 필수 항을 정확하게 추정할 수 있는 동시에 일부 If Possible 항을 감지하고 추정할 수 있습니다.
의미 있는 사전 분포를 모형의 모수에 적용하기 위해 반응과 요인이 특정한 특성을 갖도록 조정됩니다(DuMouchel and Jones, 1994, Section 2.2).
다음 표기를 고려하십시오.
• X는 반응 시뮬레이션에 정의된 모형 행렬입니다.
• K는 다음과 같은 값을 갖는 대각 행렬입니다.
– k = 0(필수 항의 경우)
– k = 1(If Possible 주효과, 검정력, 3수준 이상의 범주형 요인과 관련된 교호작용의 경우)
– k = 4(다른 모든 If Possible 항의 경우)
If Possible 모수의 벡터에 설정된 사전 분포는 평균 벡터가 0이고, 대각 공분산 행렬의 대각 항목이 1/k2인 다변량 정규 분포입니다. 따라서 k2 값은 해당 모수의 사전 분산에 대한 역수입니다.
k의 값은 경험적으로 결정됩니다. If Possible 주효과, 검정력, 자유도가 2 이상인 교호작용의 사전 분산은 1입니다. 다른 If Possible 항의 사전 분산은 1/16입니다. DuMouchel and Jones(1994) 표기에서 k = 1/t입니다.
If Possible 항에 대한 가중치를 제어하려면 빨간색 삼각형 메뉴에서 고급 옵션 > 사전 모수 분산을 선택합니다. 자세한 내용은 고급 옵션 > 사전 모수 분산에서 확인하십시오.
모수에 대한 사후 분포에는 공분산 행렬 (X¢X + K2)-1이 있습니다. 베이지안 D-최적 설계는 사후 공분산 행렬의 역에 대한 행렬식을 최대화하여 생성됩니다.
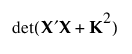
I-최적
I-최적 설계는 설계 공간에 대해 예측 평균 분산을 최소화합니다. 1차 실험 목표가 계수 추정이 아니라 다음을 수행하는 것이라면 I-최적 기준이 D-최적보다 더 적합합니다.
• 반응 예측
• 최적의 작동 조건 결정
• 설계 공간에서 반응이 허용 가능한 범위 내에 속하는 영역 결정
이 경우에는 정확한 반응 예측이 정확한 모수 추정보다 우선합니다.
설계 공간의 x0 지점에서 미지의 오차 분산에 대한 예측 분산은 다음과 같이 계산할 수 있습니다.
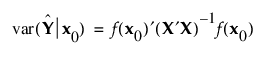
X는 반응 시뮬레이션에 정의된 모형 행렬입니다.
I-최적 설계는 전체 설계 공간에 대해 예측 분산의 적분 I를 최소화합니다. 여기서 I는 다음과 같이 지정됩니다.
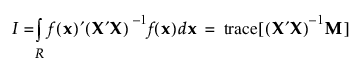
M은 적률 행렬입니다.
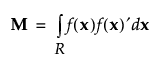
자세한 내용은 반응 시뮬레이션에서 확인하십시오.
적률 행렬은 설계에 의존하지 않으며 미리 계산할 수 있습니다. 행 벡터 f (x)¢는 1 다음에 가정된 모형에 해당하는 효과가 나옵니다. 예를 들어 연속형 요인이 두 개 있는 완전 2차 모형의 경우 f (x)¢는 다음과 같이 정의됩니다.
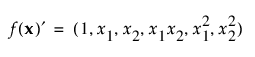
A-최적
특정 모형 효과를 강조하려는 경우 A-최적 설계를 사용합니다. A-최적 설계를 사용하면 모형 모수에 가중치를 할당할 수 있습니다. 이러한 가중치는 A-최적 기준에서 설계를 선택하기 위해 사용됩니다. 결과 설계는 가중치가 낮은 항보다 가중치가 높은 항에 대한 추정값의 분산을 낮추는 요인 조합에 더 중점을 둡니다. 예를 들어 다른 교호작용을 추정하는 것보다 더 중요한 교호작용 그룹이 있습니다. 주요 교호작용에 대한 가중치를 높여 다른 교호작용에 비해 추정값의 분산을 낮출 수 있습니다.
A-최적 기준은 모형 계수 추정값의 공분산 행렬에 대한 대각합을 최소화합니다. 대각합은 행렬에서 주대각 요소의 합입니다. A-최적 설계는 회귀 계수 분산의 합을 최소화합니다.
베이지안 I-최적
베이지안 I-최적 설계는 설계 영역에 대해 필수 항과 If Possible 항에 대한 평균 예측 분산을 최소화합니다.
다음 표기를 고려하십시오.
• X는 반응 시뮬레이션에 정의된 모형 행렬입니다.
• K는 다음과 같은 값을 갖는 대각 행렬입니다.
– k = 0(필수 항의 경우)
– k = 1(If Possible 주효과, 검정력, 3수준 이상의 범주형 요인과 관련된 교호작용의 경우)
– k = 4(다른 모든 If Possible 항의 경우)
If Possible 모수의 벡터에 설정된 사전 분포는 평균 벡터가 0이고, 대각 공분산 행렬의 대각 항목이 1/k2인 다변량 정규 분포입니다. k 값에 대한 자세한 내용은 베이지안 D-최적에서 확인하십시오.
x0 지점에서 예측값의 사후 분산은 다음과 같습니다.
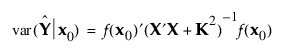
베이지안 I-최적 설계는 설계 영역에 대해 다음과 같이 평균 예측 분산을 최소화합니다.
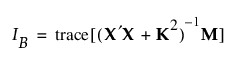
M은 적률 행렬입니다. 자세한 내용은 반응 시뮬레이션에서 확인하십시오.
별칭 최적
별칭 최적은 가정된 모형에 있는 효과와 모형에 없지만 잠재적 활성 상태인 효과 사이의 별칭 관계를 최소화하려고 합니다. 모형에 없지만 잠재적 관심 대상인 효과를 별칭 효과라고 합니다. 별칭-최적 설계에 대한 자세한 내용은 Jones and Nachtsheim(2011b)에서 확인하십시오.
구체적으로 X1을 반응 시뮬레이션에서 정의된 가정된 모형의 항에 해당하는 모형 행렬로 지정하겠습니다. 설계는 별칭 효과에 해당하는 모형을 정의합니다. X2로 별칭 효과에 대한 모형 항 행렬을 나타냅니다.
별칭 행렬은 다음과 같이 정의된 행렬 A입니다.
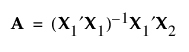
별칭 행렬의 항목은 모형 항 추정값과 관련된 편향 정도를 나타냅니다. 별칭 행렬의 파생에 대한 자세한 내용은 별칭 행렬에서 확인하십시오.
A 에 있는 항목의 제곱합은 편향에 대한 요약 지표를 제공합니다. 이 제곱합은 다음과 같이 대각합으로 나타낼 수 있습니다.
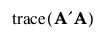
대각합 기준을 감소하는 설계는 일반적으로 D-최적 설계보다 D 효율도가 낮습니다. 결과적으로 별칭 최적은 D 효율도의 하한에 따라 A¢A의 대각합을 최소화하려고 합니다. D 효율도의 정의는 최적 기준에서 확인하십시오. D 효율도의 하한은 "고급 옵션"에서 D 효율도 가중치를 지정하여 구할 수 있습니다. 자세한 내용은 고급 옵션 > D 효율도 가중치에서 확인하십시오.