붓스트랩에 대한 통계 상세 정보
이 섹션에는 붓스트랩에 대한 통계 상세 정보가 포함되어 있습니다.
부분 가중치에 대한 통계 상세 정보
이 섹션에서는 붓스트랩 분석에서 부분 가중치를 계산하는 방법을 설명합니다. 부분 가중치 옵션은 베이지안 붓스트랩(Rubin 1981)을 기반으로 합니다. 하나의 관측값이 주어진 붓스트랩 표본에 나타나는 횟수를 붓스트랩 가중치라고 합니다. 단순 붓스트랩에서는 각 붓스트랩 표본에 대한 붓스트랩 가중치가 단순 랜덤 복원 표집 방식으로 결정됩니다.
베이지안 방법에서는 표집 확률이 알 수 없는 모수로 처리되며 무정보 사전 분포를 사용하여 확률의 사후 분포를 구합니다. 확률 추정값은 이 사후 분포에서 표집을 통해 구합니다. 이러한 추정값은 붓스트랩 가중치를 생성하는 데 사용됩니다.
• 형상 모수가 (n - 1)/n이고 척도 모수가 1인 감마 분포의 n개 값을 포함하는 벡터를 무작위로 생성합니다.
참고: Rubin 연구 자료(1981)에서는 감마 형상 모수로 1을 사용합니다. JMP에서 사용되는 형상 모수는 부분 가중치의 평균 및 분산이 단순 붓스트랩 가중치의 평균 및 분산과 같도록 합니다.
• n개 값의 합인 S를 계산합니다.
• n개 값의 벡터에 N / S를 곱해서 부분 가중치를 계산합니다. 여기서 N은 행 수 또는 빈도 합(빈도 변수가 지정된 경우)과 같습니다.
참고: 분석에 빈도 변수가 지정된 경우에는 행별로 감마 분포의 형상 모수에 빈도 값을 곱하십시오. 빈도 변수 값의 합은 1보다 커야 합니다. 그러면 형상 모수가 fi(N - 1)/N과 같아집니다. 여기서 fi는 i번째 행의 빈도 값이며 N은 빈도 값의 합과 같습니다.
이 절차에서는 붓스트랩 표집의 평균 및 분산이 단순 붓스트랩 가중치의 평균 및 분산과 같도록 각 행의 부분 가중치를 척도화합니다. 각 붓스트랩 표본의 부분 붓스트랩 가중치는 양수이고, 합은 n이 되며, 평균은 1이 됩니다.
편향 수정 백분위수 구간에 대한 통계 상세 정보
이 섹션에서는 붓스트랩 결과 테이블에서 "분포" 스크립트를 실행하면 "붓스트랩 신뢰 한계" 보고서에 표시되는 BC(편향 수정) 신뢰 구간의 계산 방법을 설명합니다. 편향 수정 백분위수 구간은 붓스트랩 분포에서 백분위수 구간의 비대칭성 설명 능력을 향상시킵니다. 자세한 내용은 Efron 연구 자료(1981)에서 확인하십시오.
표기
• p* - 관심 있는 통계량의 추정값이 원래 추정값보다 작거나 같은 붓스트랩 표본의 비율입니다.
• z0 - 표준 정규 분포의 p* 분위수입니다.
• zα - 표준 정규 분포의 a 분위수입니다.
편향 수정 신뢰 구간의 끝점
(1 - a) 편향 수정 신뢰 구간의 끝점은 붓스트랩 분포의 분위수로 주어집니다.
• 하한점은 다음 분위수입니다.
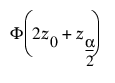
• 상한점은 다음 분위수입니다.